分类目录归档：COMSOL多物理场仿真

基于comsol的多物理场仿真

新能源储能核心技术解析：电池热失控机理、热管理设计与有限元仿真实操

发表评论

随着我国新能源行业的飞速崛起，电池储能作为光伏、风电等可再生能源消纳的核心支撑，其安全性与稳定性成为行业发展的重中之重。在电池储能系统的研发投入中，电池热管理与热失控机理研究占据着核心地位——热失控是电池最严重的安全隐患，而科学的热管理设计的核心目标，就是抑制热失控的发生与传播，有限元仿原则为二者的研究提供了高效、精准的技术手段。

今天，我们就从机理、设计、仿真三个维度，拆解电池热失控与热管理的核心逻辑，助力大家快速掌握相关核心技术。

一、先搞懂核心：电池热失控的机理的本质的“恶性循环”

电池热失控，本质上是电池内部热量产生与散热失衡，引发的一系列不可逆的链式反应，最终导致热量、可燃气体快速释放，甚至引发起火、爆炸的极端现象，其核心是“热量累积-反应加剧-热量暴增”的恶性循环，并非突然发生，而是分为五个循序渐进的阶段，且不同类型电池的触发路径略有差异（如锂离子电池与铅酸电池的热失控诱因不同）。

1. 热失控的核心触发条件

无论是锂离子电池还是铅酸电池，热失控的触发都离不开三大核心条件，满足其一便可能启动链式反应：

  • 热滥用：最常见诱因，包括环境高温、电池内部短路（如极片毛刺刺穿隔膜）、外部短路（如线路故障）、过度充电/放电，这些都会导致电池温度异常升高，突破安全阈值。例如铅酸电池严重失水后，内阻增大、产热增加，会进一步降低析气过电位，析气量增多释放更多热量，形成恶性循环；锂离子电池则可能因高温导致隔膜熔毁，引发内部短路。
  • 机械滥用：电池受到挤压、穿刺、碰撞等外力冲击，导致电极、隔膜破损，引发内部短路，进而产生大量焦耳热，触发热失控。比如新能源汽车碰撞事故中，电池包受损后往往会伴随热失控风险。
  • 电滥用：过度充电会导致电池内部锂析出，形成锂枝晶，刺穿隔膜引发内部短路；过度放电则会导致电极结构破坏，产生不可逆反应，释放热量。

2. 热失控的完整链式反应过程

以应用最广泛的锂离子电池为例，热失控的链式反应可清晰分为五个阶段，且每个阶段都有明确的温度特征与反应现象，对应典型的“温度爬坡-突变-回落”曲线：

  1. 阶段1：预热阶段（温度＜100℃）——电池因外部诱因（如充电发热、环境高温）温度缓慢上升，此时电池内部仅发生轻微副反应，产热较少，散热系统可正常应对，无明显异常。
  2. 阶段2：反应启动阶段（100℃-150℃）——温度达到100℃左右时，电池电解液开始蒸发，产生少量可燃气体；随着温度升至150℃，隔膜（通常为聚烯烃材质）开始熔化、收缩，电池内部出现微短路，产热速率加快，温度上升速度明显提升。
  3. 阶段3：热失控启动阶段（150℃-200℃）——隔膜完全破损，正负极直接接触，发生剧烈内部短路，产生大量焦耳热；同时，正极材料分解，释放氧气与热量，与电解液反应生成更多可燃气体（如CO、CH4），电池内部压力开始升高，安全阀准备开启。
  4. 阶段4：热失控爆发阶段（200℃-800℃）——温度突破200℃后，负极材料与电解液发生剧烈反应，释放大量热量，温度呈指数级上升（最快可达每秒7℃），最高温度可突破800℃；内部压力超过安全阀临界值，安全阀开启，可燃气体大量泄漏，与空气接触后易引发燃烧。值得注意的是，热失控过程中，电池产气会导致外壳膨胀，膨胀力累积还会减小相邻电池的接触热阻，加速热失控传播。
  5. 阶段5：衰减阶段（温度＞800℃后）——随着可燃气体燃烧、热量扩散，电池内部反应逐渐减弱，温度缓慢回落，但此时电池已完全损坏，且燃烧产生的高温可能引发周边电池连锁反应，导致热失控扩散。

核心总结：热失控的本质是“热量产生＞热量散失”的恶性循环，一旦启动，反应速度极快、破坏力极强，因此，电池热管理系统的核心任务，就是打破这个循环，要么提前散热，要么阻断热传播。

二、防御之道：电池热管理的常见设计方式

电池热管理系统（BTMS）的核心目标是：将电池工作温度控制在15℃-35℃的“黄金温区”，避免局部过热，抑制热失控发生；若热失控已启动，则阻断其在电池模组间的传播，降低事故损失。

结合当前行业应用现状，常见的热管理设计主要分为四大类，各有适配场景与优劣。

1. 风冷设计：低成本基础方案，适配中低功率场景

风冷是最基础、成本最低的热管理方式，核心原理是利用空气流动带走电池表面的热量，分为自然对流风冷与强制对流风冷两种：

  • 自然对流风冷：无需额外动力设备，仅通过电池包的风道设计，利用热空气上升、冷空气下沉的自然对流原理，实现热量散发。结构简单、维护方便、成本极低，但散热效率有限，受环境温度影响大，仅适用于低功率储能设备（如小型家用储能、低速电动车电池）。
  • 强制对流风冷：在自然对流基础上，增加风扇、鼓风机等动力设备，强制推动空气流过电池表面，加速热量散发。通过优化风道设计、采用智能风扇调速技术，可提升散热效率，适配中低功率储能模组，但仍存在散热均匀性差、高温环境下效果不佳的问题。

适配场景：小型储能设备、入门级新能源汽车，对成本敏感、散热需求较低的场景。

2. 液冷设计：主流高效方案，适配中高功率场景

液冷是目前新能源储能、新能源汽车领域应用最广泛的热管理方式，核心原理是利用冷却液（如乙二醇水溶液、专用冷却液）的高比热容、高导热性，通过管道与电池接触，高效带走热量，分为直接冷却与间接冷却两种，其中间接冷却因安全性更高，成为行业主流：

  • 间接冷却：通过冷却板（通常为铝合金材质）将电池与冷却液隔开，冷却板与电池紧密贴合，电池热量先传递到冷却板，再由冷却液循环带走，经散热器与外界空气热交换后，冷却液循环复用。例如特斯拉Model 3采用蛇形冷却管设计，冷却管紧密贴合电池模组，大幅提升散热效率。
  • 直接冷却：冷却液直接与电池电极或电芯接触，散热效率更高，但对冷却液的兼容性、绝缘性要求极高，一旦泄漏会导致电池短路，目前仅在少数高端场景试点应用。

液冷设计的优势的散热效率高、温度控制均匀，可适配高温环境与高功率储能设备（如大型电站储能、高端新能源汽车），但结构复杂、成本较高，核心技术难点在于冷却系统的密封性与冷却液的选型。

3. 相变材料（PCM）热管理设计：被动散热补充方案

相变材料（如石蜡、水合盐等）的核心特性是：在特定温度下会发生相变（固态→液态），吸收大量热量，且相变过程中温度保持稳定，可快速抑制电池温度升高；当电池温度降低时，相变材料从液态变回固态，释放热量，维持电池温度稳定。

实际应用中，相变材料通常填充在电池模组之间或包裹在电池表面，作为风冷、液冷系统的补充——当电池突发产热（如快充、短时过载）时，相变材料快速相变吸热，避免温度骤升；正常工况下，配合主动散热系统，提升温度控制的稳定性。其局限性在于相变材料的热导率较低，单独使用难以满足高功率设备的散热需求，且多次相变后性能会出现衰退，因此常与液冷系统结合使用。

4. 热泵热管理设计：双向控温，适配极端环境

热泵技术基于逆卡诺循环原理，可实现热量的双向传递，既能制冷（夏季给电池降温），也能制热（冬季给电池预热），完美解决了极端温度环境下电池性能衰减的问题，目前在高端储能设备与新能源汽车中逐渐普及。

热泵系统主要由压缩机、冷凝器、蒸发器、膨胀阀等部件组成，通过调节制冷剂的循环方向与流量，精准控制电池温度——寒冷天气下，热泵从外界吸收热量，给电池预热，使其快速达到工作温度；炎热天气下，热泵将电池热量排出，维持温度稳定。其优势是控温精准、能耗低，可适配北方低温、南方高温等极端环境，但结构复杂、成本较高。

补充说明：除了上述主流设计，目前行业还在研发耦合热阻网络的热管理方案，通过建立电池模组的热阻网络，精准描述热量传导路径，结合机械结构设计，抑制热失控传播，进一步提升电池安全性。

三、实操核心：有限元仿真在电池热失控中的具体实施步骤

在电池热失控与热管理的研发中，有限元仿真是高效、低成本的核心工具——无需搭建实体原型，即可精准模拟热失控的发生、传播过程，验证热管理设计的有效性，优化结构参数。目前主流的有限元仿真软件包括COMSOL、Ansys Fluent、LS-DYNA等，其中COMSOL适用于多物理场耦合仿真，Ansys Fluent更适用于热流场分析，实操步骤可分为“前期准备-模型构建-边界条件设置-仿真求解-结果分析”五大环节，结合行业实操经验，详细拆解如下。

1. 前期准备：明确仿真目标与参数采集（核心前提）

仿真前的准备工作直接决定仿真结果的准确性，核心是明确目标、采集关键参数，具体分为两步：

  • 明确仿真目标：确定仿真核心需求，是模拟“热失控的触发过程”“热失控在模组内的传播规律”，还是“热管理系统的散热效果”；同时确定仿真对象（单体电池、电池模组或整包），例如小型储能可聚焦单体电池，大型电站储能需模拟模组级热失控传播。
  • 采集关键参数：参数的准确性是仿真的核心，需采集三类核心参数，且需结合电池实际特性调整：
    • 几何参数：电池的尺寸（长、宽、高）、电极厚度、隔膜厚度、电池模组的排列方式、热管理结构（如冷却管尺寸、风道尺寸）等，需与实际原型一致。
    • 材料参数：电池各组件（正极、负极、电解液、隔膜、外壳）的热导率、比热容、密度，以及热失控过程中材料的相变参数（如隔膜熔点、相变材料相变温度）；若涉及耦合仿真，还需采集电化学参数、材料力学参数（如外壳弹性模量）。值得注意的是，材料参数会随温度变化，需设置温度相关的参数函数，例如电解液的导热系数在温度突破220℃后会显著升高，需通过函数精准模拟。
    • 工况参数：仿真场景的环境温度、充电/放电倍率、外部热源功率（如模拟穿刺触发热失控时的热源参数）、热管理系统的工作参数（如液冷流速、风扇转速）等，需贴合实际应用场景（如储能电站的环境温度通常设置为20℃，模拟高温工况可设置为45℃）。

2. 模型构建：几何建模与网格划分（仿真基础）

模型构建是仿真的核心环节，需借助有限元软件的建模模块，还原电池与热管理系统的真实结构，核心分为两步：

  • 几何建模：根据采集的几何参数，在软件中绘制三维几何模型，重点注意两点：一是简化冗余结构（如电池内部极片的细微纹路，可适当简化，避免网格数量过多，降低计算成本）；二是精准还原关键结构，如热管理系统的冷却管、风道、相变材料填充区域，以及电池的安全阀位置（模拟热失控时的产气泄漏）。对于模组级仿真，需绘制电池单体、相邻电池的间隙、硅胶隔热层等结构，还原模组的真实排布。
  • 网格划分：网格是有限元仿真的“计算单元”，网格质量直接影响仿真精度与计算效率，核心原则是“关键区域加密，非关键区域简化”：
    • 加密区域：电池核心区域（正负极、电解液）、热失控易发生区域（如极耳附近，仿真发现此处常为最高温度点）、热管理系统与电池接触区域（如冷却板贴合处），采用细网格，提升仿真精度。
    • 简化区域：电池外壳、模组支架等非核心区域，采用粗网格，减少计算量。
    • 网格类型：通常采用四面体网格或六面体网格，其中六面体网格的计算精度更高，适用于结构规则的电池（如方形电池）；四面体网格适用于结构复杂的模组（如软包电池模组）。网格划分后，需检查网格质量，避免出现扭曲、畸形网格，否则会导致仿真结果失真。

3. 边界条件与载荷设置：还原真实仿真场景（核心关键）

边界条件与载荷设置，本质是模拟电池热失控的触发场景与热管理系统的工作状态，需结合仿真目标精准设置，核心分为三类设置：

  • 热边界条件：
    • 环境边界：设置环境温度（如20℃），以及电池与环境的换热方式（自然对流、强制对流），输入对流换热系数（自然对流通常为5-10 W/m2⋅Km²·Km2⋅K，强制对流根据风扇转速调整）；若涉及热辐射，可设置辐射换热系数，通常忽略热辐射对仿真结果的影响（占比极小）。
    • 内部热源设置：模拟热失控的触发，需在电池核心区域设置热源，热源功率根据热失控阶段调整——预热阶段产热少，可设置较低功率；热失控爆发阶段，需设置随温度变化的热源函数，贴合链式反应的产热规律（如基于Arrhenius公式，模拟副反应放热随温度的变化）。若模拟穿刺触发热失控，可通过Fluent Profile格式的热源模拟穿刺点的产热。
  • 力学边界条件（若涉及耦合仿真）：若需模拟热失控过程中电池的膨胀、外壳变形，需设置力学边界，如电池外壳的固定约束、相邻电池的接触约束，输入材料的力学参数（如弹性模量、泊松比）；同时，将热阻网络计算获得的电池温度和内部压力参数，作为动态边界条件施加于电池外壳，实现热-力耦合仿真，模拟电池膨胀与热失控传播的相互影响。
  • 热管理系统载荷设置：若仿真热管理系统的效果，需设置热管理系统的工作参数——液冷系统设置冷却液的入口温度、流速；风冷系统设置风扇的风速、风向；相变材料设置相变温度与相变潜热；热泵系统设置制冷剂的循环参数。例如，模拟液冷系统时，可设置冷却液入口温度为25℃，流速为0.5 m/s，贴合实际工作状态。

补充技巧：可设置“阶段切换触发器”，当某个网格单元的温度达到临界值（如隔膜熔点150℃、热失控启动温度200℃）时，自动激活下一阶段的控制方程，实现热失控各阶段的自然过渡，避免仿真结果出现断层。例如，当温度突破250℃时，开启泄压阀模型，关闭隔膜熔化计算，模拟热失控时的产气泄漏过程。

4. 仿真求解：参数调试与计算（实操重点）

求解阶段的核心是设置求解器参数，调试仿真收敛性，避免出现计算发散、结果失真的问题，具体步骤：

  • 选择求解器：根据仿真类型选择合适的求解器——纯热分析（如热失控温度传播）可选择热传导求解器；热-电耦合（如内部短路产热）选择热电耦合求解器；热-力-电多物理场耦合（如热失控+电池膨胀）选择多物理场耦合求解器。热失控涉及多物理场强耦合时，建议采用全耦合求解器，避免遗漏关键相互作用，否则可能导致温度峰值计算偏差（偏差可达10%以上）。
  • 设置求解时间与时间步长：热失控的过程较快（通常为几分钟），求解时间需覆盖完整的热失控阶段（如0-300秒）；时间步长采用“变步长”，平稳阶段（如预热阶段）用较大步长（如1秒），节省计算时间；温度突变阶段（如热失控爆发阶段）用极小步长（如0.01秒），确保捕捉到温度骤升的细节，避免计算发散。若全用自动步长，可能在温度突变点出现仿真发散，影响结果准确性。
  • 调试收敛性：若仿真出现不收敛（如温度无限制升高、计算中断），需检查三个关键点：一是网格质量（是否有畸形网格）；二是边界条件（是否设置合理，如热源功率是否过高）；三是材料参数（是否随温度变化，如导热系数是否设置正确）。可通过加密关键区域网格、调整热源功率、优化材料参数函数等方式，提升收敛性。

5. 结果分析：提取关键信息，指导设计优化（仿真目的）

仿真求解完成后，需提取关键结果，分析热失控规律与热管理系统的效果，为实际研发提供指导，核心分析内容包括：

  • 热失控相关分析：
    • 温度场分析：提取电池内部、模组内的温度分布云图，分析温度变化曲线，确定热失控的触发时间、温度峰值、传播速度（如模组内相邻电池的热失控延迟时间）；重点关注极端位置的温度，如边缘电池与中间电池的温度差异——边缘电池因散热路径单一，温度上升更快，危险性更高，这一结论可指导模组排列设计。
    • 产气与压力分析：提取电池内部压力变化曲线、可燃气体泄漏速率，分析安全阀的开启时间与效果，优化安全阀的设计参数（如开启压力）；同时分析膨胀力的累积规律，优化模组间隙与隔热设计，抑制热失控传播。
  • 热管理系统效果分析：
    • 散热效率分析：提取电池在不同工况下的温度变化，判断热管理系统是否能将温度控制在黄金温区；例如，模拟高温工况（45℃）下，液冷系统是否能将电池温度控制在35℃以下，风冷系统的散热效率是否满足需求。
    • 优化方向：若热管理效果不佳（如局部温度过高），可通过调整热管理参数（如液冷流速、冷却管布局、相变材料填充量），重新仿真验证，直至达到设计要求。例如，仿真发现风速低于0.5 m/s时，电池温度持续上升，热失控难以避免，可将强制风冷的风速设置为≥0.5 m/s，提升散热效果。
  • 预警信号分析：提取电池电压、温度的变化规律，分析热失控前的预警信号——仿真显示，电压变化通常比温度变化提前40秒左右，可基于这一规律，优化热失控预警算法，为实际安全监测提供依据。

四、行业总结与展望

随着新能源储能向高功率、大容量、长寿命方向发展，电池热失控的防控与热管理技术的优化，成为行业突破的核心瓶颈。热失控的本质是“热量累积的恶性循环”，而科学的热管理设计（液冷、风冷、相变材料等）是阻断这一循环的关键，有限元仿原则为二者的研发提供了高效、精准的技术支撑，大幅降低研发成本、缩短研发周期——从参数采集、模型构建到结果分析，每一个环节的精准把控，都能为实际产品设计提供可靠的理论依据。

目前，行业已开始探索“热阻网络+有限元”的耦合仿真方法，结合人工智能技术，实现热失控的精准预测与热管理系统的智能优化；未来，随着仿真技术的升级与材料技术的突破，将逐步实现“提前预警-主动防控-阻断传播”的全流程安全防护，推动新能源储能行业的安全、健康发展。

如果你正在从事电池热管理与热失控相关研发，欢迎在评论区交流仿真实操中的难点（如网格划分、收敛性调试），后续将结合具体案例，拆解更多实操技巧！

别再被CFD壁面滑移搞晕！一篇看懂 COMSOL 里 7 种滑移，生活生产全是例子

发表评论

做CFD仿真，尤其是用COMSOL的工程师，大概率都在壁面边界条件里纠结过：

默认无滑移算出来不对，一开滑移又懵了——

滑移、电渗滑移、渗漏滑移、Navier滑移、非线性Navier滑移、Hatzikiriakos滑移、渐进滑移……

这么多“滑移”，到底啥区别？都用在哪？

这篇不讲复杂公式，用生活+生产里看得见的场景，把滑移讲得明明白白。

一、先搞懂：到底什么是“壁面滑移”？

我们从小在流体力学书里学到的都是：

流体碰到固体壁面，会牢牢“粘”在壁面上，速度为0 → 无滑移边界

但现实世界根本没这么理想。

很多情况下，流体并不会粘死在壁面，而是会贴着壁面“滑过去”，这就叫壁面滑移。

可以用三个生活场景一秒理解：

1. 无滑移：就像鞋底粘在湿滑的地板上

水流紧贴管壁，一点不滑，完全被壁面“拽住”。

大部分宏观管道流动、自来水、空调风管，都可以近似无滑移。

2. 完全滑移：像冰壶在冰面上自由滑行

流体和壁面之间几乎没有摩擦，想怎么滑就怎么滑。

3. 部分滑移：像小孩穿着袜子在地板上蹭

能滑一点，但又不是完全没阻力，滑得快慢和阻力有关。

微流控、超疏水表面、稀薄气体，基本都是这种。

一句话总结：

滑移，就是流体在壁面“打滑”的程度。

滑移越强，壁面对流体拖拽越小；滑移越弱，越接近粘死。

二、7种滑移边界：概念+生活/生产场景，一看就会

1. 滑移（自由滑移 / 理想滑移）

概念

最简单的一种滑移：

法向流体穿不过壁面，但切向完全没有剪切阻力，想怎么滑就怎么滑。

≈ 壁面是“超级冰面”。

生活/工程场景

  • 风洞试验中，把对称面设为自由滑移，减少计算域
  • 理想无粘流动，比如高速飞行器外掠，忽略壁面粘性
  • 波浪仿真、液面波动，气液界面常用近似自由滑移

一句话记

没摩擦，随便滑，理想情况用它。

2. 电渗滑移

概念

不是流体自己滑，而是电场在“推着”流体滑。

壁面带电荷，附近形成双电层，电场一施加，离子拖拽整体流体一起滑移。

生活/生产场景

  • 微流控芯片里的“电渗泵”，不用机械叶轮就能送液
  • 核酸检测芯片、PCR芯片、Lab-on-a-Chip
  • 毛细管电泳、药物筛选、单细胞捕获
  • 印刷电子、喷墨里的微液滴操控

一句话记

电场一上场，流体自己滑，微流控必备。

3. 渗漏滑移（渗透滑移）

概念

普通滑移只允许“切向滑”，渗漏滑移还允许法向穿过壁面。

一边滑，一边渗，壁面是“可透气透水的滑移面”。

生活/生产场景

  • 过滤膜、净水器、海水淡化
  • 人体组织、血管壁、药物渗透
  • 多孔催化剂、燃料电池气体扩散层
  • 岩石油水渗流、土壤地下水流动

一句话记

又滑又渗，多孔介质必选。

4. Navier 滑移（线性Navier滑移）

概念

最经典、最常用的线性部分滑移。

滑移速度 ∝ 壁面剪切应力，比例系数叫滑移长度。

滑移长度越大，滑得越狠。

生活/生产场景

  • 微通道、微喷嘴内的流动（几十~几百微米）
  • 超疏水表面、荷叶效应、不粘涂层
  • 稀薄气体，如高空飞行器、真空管道
  • 润滑、轴承油膜、微小间隙流动

一句话记

滑多少，看剪切，微纳流动首选它。

5. 非线性Navier滑移

概念

滑移速度和剪切应力不是直线关系，而是非线性（幂律、指数等）。

剪切越强，滑移可能突然变大或变小。

生活/生产场景

  • 高剪切下的微流控，如高速喷墨
  • 高分子溶液、涂料、胶水
  • 强剪切下壁面滑移明显增强的流动

一句话记

剪切越强滑得越离谱，非牛顿流体用它准没错。

6. Hatzikiriakos 滑移

概念

专门给粘弹性流体、高分子熔体设计的滑移模型。

考虑聚合物分子链在壁面“解缠”后才开始滑移，有明显临界剪切应力。

生活/生产场景

  • 塑料挤出、注塑成型、3D打印耗材
  • 吹膜、拉丝、化纤纺丝
  • 热熔胶、橡胶加工、聚合物加工

一句话记

塑料熔体一挤就滑，高分子加工专用。

7. 渐进滑移

概念

滑移长度不是常数，而是沿着壁面逐渐变化。

比如从“几乎不滑”慢慢变成“很滑”。

生活/生产场景

  • 梯度润湿性表面，一端亲水一端疏水
  • 功能梯度涂层、仿生表面
  • 沿程粗糙度渐变的微通道
  • 智能控流、微流体整流

一句话记

壁面性能不均匀，滑移一路慢慢变。

三、一张表速查：7种滑移怎么选

滑移类型核心特点关键参数典型场景
滑移（自由滑移）切向无摩擦，自由滑动无额外参数理想无粘流、对称面、液面
电渗滑移电场驱动双电层滑移电场、Zeta电位微流控、电渗泵、生物芯片
渗漏滑移切向滑移+法向渗透渗透率、滑移长度过滤膜、多孔介质、渗流
Navier 滑移滑移与剪切线性相关滑移长度微通道、超疏水、稀薄气体
非线性Navier滑移滑移与剪切非线性关系非线性系数高剪切、非牛顿流体、涂料
Hatzikiriakos滑移高分子解缠滑移，有临界应力临界剪切应力塑料注塑、挤出、熔体流动
渐进滑移滑移长度沿壁面渐变滑移长度分布梯度表面、功能涂层、仿生流道

四、读完这篇，你再也不会乱设滑移了

  • 做普通理想流动 → 自由滑移
  • 做微流控用电场 → 电渗滑移
  • 做过滤、多孔介质 → 渗漏滑移
  • 做微通道、超疏水 → Navier滑移
  • 做高剪切、胶水涂料 → 非线性Navier
  • 做塑料注塑挤出 → Hatzikiriakos
  • 做梯度功能表面 → 渐进滑移

如果你是做COMSOL多物理场仿真，这篇可以直接当滑移边界条件选择手册。

如何读懂传质仿真的”视觉语言”

发表评论

传质仿真完成后，你会得到海量的数据——浓度场、通量矢量、反应速率、温度耦合分布……但数据不等于信息。本章将带你掌握传质仿真结果的专业解读方法，让你从”看图说话”进阶到”看图说机理”。

一 浓度云图：传质仿真的”基础款”

什么是它？

浓度云图（Concentration Contour Plot）是最直观的传质结果，用颜色梯度表示物质在空间中的分布。从深蓝到鲜红，就像气象云图显示降雨强度一样，显示浓度的高低。

典型应用场景：

应用领域云图特征关键解读点
氢燃料电池阴极氧气浓度从入口到出口递减识别”缺氧区”（蓝色区域），优化流道设计
碳捕集吸收塔CO₂浓度在液相中从气液界面向内递减判断液相利用率，识别”未反应核”
木材干燥含水率从表面向中心递减，随时间推移观察干燥锋面的推进速度，预测开裂风险
药物控释药物浓度从载体中心向外梯度释放评估突释效应（initial burst）和缓释持续性

专业解读技巧：

  1. 边界层厚度识别：在气液或固液界面附近，浓度梯度最大的薄层就是传质边界层。层越厚，传质阻力越大。在燃料电池中，理想边界层厚度应小于50微米。
  2. 死区识别：如果某个角落浓度长期保持不变（与主体浓度相同），说明存在流动死区。这在化工反应器设计中是大忌，会导致反应物停留时间分布不均。
  3. 对称性检验：对于对称几何，浓度分布应该对称。如果出现不对称，可能是网格质量差或数值发散的信号。

2024年实战案例：激光刻蚀质子交换膜

Nature Communications 2024年发表的研究中，研究团队使用µ-CT扫描真实的膜电极（MEA）三维结构，导入COMSOL进行多物理场仿真。浓度云图显示：经过激光刻蚀处理的膜电极，氧气浓度分布更加均匀，局部缺氧区面积减少了40%，这直接解释了为什么功率密度提升了25%。

二 通量矢量图：看见”物质的流动”

什么是它？

通量矢量图（Flux Vector Plot）用箭头表示物质流动的方向和强度。箭头的长度代表通量大小，方向代表扩散或对流的路径。

核心数学表达：J=−D∇c+cu\mathbf{J} = -D \nabla c + c\mathbf{u}J=−D∇c+cu

（扩散通量 + 对流通量）

典型解读场景：

场景A：电化学系统中的离子迁移

在电解制氟的仿真中（2024年研究），通量矢量图揭示了惊人的发现：

  • 主通量路径：HF分子从阳极产生，向阴极扩散消耗
  • 二次通量：电场引起的电迁移（离子在电场中的定向移动）占总通量的30%
  • 涡流效应：阴极产生的氢气气泡上升，带动电解液形成旋转涡流，显著增强了对流传质

解读要点：箭头密集区是高通量区，箭头稀疏区是传质瓶颈。如果箭头出现”回流”或”漩涡”，说明存在复杂的二次流结构。

场景B：多孔介质中的有效扩散

在多孔热化学储热材料（CaO/Ca(OH)₂系统）的仿真中，研究者通过通量矢量图发现：

  • 气体在孔隙中的实际路径比直线路径长3-5倍（曲折度效应）
  • 有效扩散系数 Deff=Dbulk⋅ετD_{eff} = D_{bulk} \cdot \frac{\varepsilon}{\tau}Deff​=Dbulk​⋅τε​，其中 ε\varepsilonε 是孔隙率，τ\tauτ 是曲折度
  • 对于分形多孔介质，分形维数越大，扩散阻力越大

实用技巧：在COMSOL或ANSYS中，可以叠加浓度云图和通量矢量图，用颜色显示浓度，用箭头显示流动方向，这种”组合视图”最能揭示传质机理。

三 时间序列动画：捕捉”瞬态之美”

为什么需要它？

很多传质过程是非稳态的——比如电池充放电时的锂离子浓度重分布、食品干燥时的湿分迁移前沿。静态图片只能显示某一时刻，而动画能揭示动态演化规律。

典型应用：

案例：牛肉腌制过程中的NaCl扩散（2024）

江南大学团队结合能谱分析（EDS）和有限元仿真，重建了真实牛肉组织（肌肉、脂肪、结缔组织）的几何模型。时间序列动画显示：

  • 0-2小时：NaCl主要在肌肉组织表面聚集，扩散前沿呈”手指状”突进
  • 2-6小时：盐分开始穿透结缔组织，但速度比肌肉慢50%
  • 6-12小时：整体浓度趋于均匀，但脂肪组织中心仍存在低盐核心区

关键参数提取：

通过动画数据拟合，得到不同组织的有效扩散系数：

  • 肌肉：1.2×10−10 m2/s1.2 \times 10^{-10} \text{ m}^2/\text{s}1.2×10−10 m2/s
  • 脂肪：0.3×10−10 m2/s0.3 \times 10^{-10} \text{ m}^2/\text{s}0.3×10−10 m2/s
  • 结缔组织：0.8×10−10 m2/s0.8 \times 10^{-10} \text{ m}^2/\text{s}0.8×10−10 m2/s

这种组织特异性的扩散数据，对于优化脉冲电场（PEF）辅助腌制工艺至关重要——研究发现，2.0 kV/cm的PEF处理可以将腌制时间缩短33%，同时提高嫩度22.9%。

四 定量曲线：从”定性好看”到”定量好用”

极化曲线（电池/燃料电池）

在氢燃料电池仿真中，**极化曲线（I-V曲线）**是核心输出：

  • 线性区（低电流）：活化极化主导，电压随电流线性下降
  • 欧姆区（中电流）：质子交换膜的欧姆电阻主导，斜率较陡
  • 浓差极化区（高电流）：传质限制主导，电压急剧跌落

关键指标提取：

  • 最大功率密度：极化曲线与功率密度曲线的交点
  • 极限电流密度：浓差极化区开始的临界点，反映传质能力的上限

2024年的激光刻蚀膜电极研究中，仿真极化曲线与实验数据的误差小于5%，验证了模型的可靠性。

突破电流密度（Breakthrough Current Density）

在燃料电池水管理仿真中，定义水淹起始电流为：当液态水饱和度在气体扩散层（GDL）中超过**20%**时的电流密度。通过参数化扫描，可以找到最优的GDL孔隙率梯度设计。

五 多物理场耦合视图：看见”隐藏的关联”

温度-浓度耦合：木材干燥案例

南京林业大学的研究显示：

  • 温度升高 → 水分扩散系数指数增加（Arrhenius关系）
  • 但温度过高 → 表面硬化（case hardening）→ 内部蒸汽压升高 → 开裂
  • 通过温度云图+含水率云图的叠加分析，确定了最优干燥曲线：升温速率2°C/小时，湿度梯度降低20%

速度-浓度耦合：燃料电池流道设计

在质子交换膜燃料电池中，流道内的气体流速分布直接影响氧气浓度分布：

  • 脊下区域（under the rib）：流速低，扩散距离长，容易缺氧
  • 流道中心：流速高，但压降大
  • 通过速度矢量图+浓度云图的耦合分析，2024年的优化设计将流道/脊宽比从1.0调整为1.5，使电流密度分布均匀性提高了18%

六 结果验证：仿真不是”电子游戏”

与实验数据对比的三种层次：

验证层次方法可信度
定性验证趋势对比（如浓度分布形状是否一致）★★☆
半定量验证特征值对比（如突破时间、平均浓度）★★★
定量验证全场数据对比（R² > 0.9）★★★★★

2024年标杆案例：激光刻蚀膜电极

研究团队将COMSOL仿真结果与µ-CT扫描的真实结构对比：

  • 几何重建精度：孔隙分辨率2.5微米
  • 电化学性能预测误差：<5%
  • 水分布预测：与同步辐射X射线成像结果吻合

验证失败怎么办？

如果仿真与实验不符，检查清单：

  1. 网格独立性：是否进行了网格敏感性分析？（建议至少3套网格对比）
  2. 边界条件：入口浓度、流量是否准确？
  3. 物性参数：扩散系数是否考虑了温度依赖性？
  4. 反应动力学：表面反应速率常数是否经过校准？

七 高级后处理技巧：让数据”说话”

1. 无量纲数分析

将仿真结果转化为无量纲数，可以实现跨尺度对比：

  • Sherwood数（Sh）：实际传质速率与纯扩散传质速率的比值，Sh=kLDSh = \frac{kL}{D}Sh=DkL​
  • Damköhler数（Da）：反应速率与传质速率的比值，Da=kreactionL2DDa = \frac{k_{reaction}L^2}{D}Da=Dkreaction​L2​

在碳捕集吸收塔中，Da>10Da > 10Da>10 表示反应控制，Da<0.1Da < 0.1Da<0.1 表示传质控制。

2. 敏感性分析（Parameter Sweep）

通过自动化的参数扫描，识别关键影响因素：

  • 在氢能储罐仿真中，研究发现孔隙率对有效扩散系数的影响比温度更敏感（指数级 vs 线性）
  • 在药物控释中，载体降解速率比初始载药量对释放曲线形状的影响更大

3. 不确定性量化（UQ）

使用蒙特卡洛方法，考虑输入参数的不确定性（如扩散系数的测量误差±10%），输出浓度的置信区间。这在核废料处置、药物安全评估等高风险领域至关重要。

八 结果呈现的艺术：如何让你的仿真图”惊艳”

色彩选择原则：

  • 避免彩虹色图（Rainbow Colormap）：人眼对蓝-红过渡不敏感，推荐使用viridis或plasma等感知均匀色图
  • 突出关键区域：使用透明度或局部放大，显示浓度边界层或反应前沿
  • 对比视图：左右并排放置优化前后的结果，差异一目了然

动画制作技巧：

  • 时间缩放：将10小时的干燥过程压缩为30秒动画，但保持关键时间节点的标注
  • 多视图同步：同时显示浓度分布、通量矢量、和平均浓度曲线，建立空间-时间关联

结语：从”看见”到”看懂”

传质仿真的结果图不仅仅是”漂亮的颜色”，它们是物理机理的可视化表达。掌握以下解读框架：

  1. 先看整体：浓度分布是否符合物理直觉？对称性如何？
  2. 再看局部：边界层、死区、通量集中区在哪里？
  3. 动态演化：瞬态过程揭示了什么机理？
  4. 定量验证：与实验数据的吻合度如何？
  5. 工程转化：结果如何指导设计优化？

当你能从一张浓度云图中读出扩散系数的大小、对流强度的影响、反应-传质的竞争关系时，你就真正掌握了传质仿真的”视觉语言”。

毕竟，在这个由分子运动构成的世界里，看见流动，就是理解变化。

新增参考文献索引：

  • Shi et al., 2025 – 牛肉腌制传质有限元分析与高光谱成像
  • Xia et al., 2019 – 多孔热化学储热材料传质细观探索
  • Jackfruit drying simulation, 2023 – 收缩变形与热质耦合模拟
  • 电解制氟多物理场仿真 – 动量-传热-传质耦合分析
  • Nature Communications 2024 – 激光刻蚀质子交换膜多物理场仿真

当咖啡遇上氢能：有限元传质仿真的奇妙世界

发表评论

从一杯手冲咖啡的萃取，到价值百亿的氢燃料电池，质量传递的数学之美无处不在

开场白：为什么你的咖啡会”淡”？

想象这样一个早晨：你精心研磨了15克埃塞俄比亚耶加雪菲，水温控制在92°C，注水手法稳如老狗——但第一口下去，味道却淡得像是洗杯水。为什么？

答案藏在传质里。

咖啡萃取本质上是水分子”绑架”咖啡粉中风味物质的过程。如果水流太快（对流太强），物质来不及扩散；如果研磨太细（扩散距离太短），又会过萃发苦。这个微妙的平衡，正是传质仿真要解决的工程问题。

而在2024-2025年，这种”咖啡哲学”正在被应用到更宏大的场景中：从固态电池的离子迁移，到碳捕集工厂的CO₂吸收，再到氢能储罐的相变传质。有限元方法（FEM）已经成为破解这些复杂传质谜题的”瑞士军刀”。

传质仿真的三大门派

在有限元的世界里，传质问题通常被归类为以下几种”武功流派”：

1. 扩散派：菲克定律的信徒

最基础的传质形式，遵循菲克定律：J=−D∇c\mathbf{J} = -D \nabla cJ=−D∇c

其中 J\mathbf{J}J 是扩散通量，DDD 是扩散系数，ccc 是浓度。这就像是咖啡粉中的风味分子在”随机漫步”，从高浓度区域向低浓度区域迁移。

核心方程（瞬态对流-扩散方程）：∂c∂t+∇⋅(uc)=∇⋅(D∇c)+R\frac{\partial c}{\partial t} + \nabla \cdot (\mathbf{u}c) = \nabla \cdot (D \nabla c) + R∂t∂c​+∇⋅(uc)=∇⋅(D∇c)+R

这个方程的左边是”变化率+对流搬运”，右边是”扩散分散+反应生成”。在有限元软件（如COMSOL、ANSYS）中，这是最基本的传质物理场接口。

2024热门应用：木材干燥的智能优化

南京林业大学的研究团队在2024年开发了一套结合近红外光谱成像和X射线CT扫描的木材传质模型。他们将真实的木材孔隙结构（平均孔隙率15%）导入有限元模型，模拟干燥过程中的水分迁移。结果显示：通过优化干燥参数（升温速率降至2°C/小时，湿度梯度降低20%），最终开裂率可以从行业平均的15%降至8%。

这不仅仅是学术游戏——中国每年因干燥缺陷损失的木材价值超过50亿元。

2. 电化学派：带电粒子的华尔兹

当传质遇上电场，事情变得有趣起来。在电池和燃料电池中，离子在电场作用下的迁移遵循能斯特-普朗克方程：Ni=−Di∇ci−ziFRTDici∇ϕ+ciu\mathbf{N}_i = -D_i \nabla c_i – \frac{z_i F}{RT} D_i c_i \nabla \phi + c_i \mathbf{u}Ni​=−Di​∇ci​−RTzi​F​Di​ci​∇ϕ+ci​u

这里多了电迁移项（第二项），其中 ziz_izi​ 是离子电荷数，FFF 是法拉第常数，ϕ\phiϕ 是电势。

2024-2025热门应用：氢燃料电池的”水管理”难题

质子交换膜燃料电池（PEMFC）有一个致命弱点：水淹。反应生成的水如果不能及时排出，会堵塞气体扩散层（GDL），导致”窒息”停机。

最新的COMSOL燃料电池模块可以模拟三相流传质——气态反应物、液态产物水、以及溶解的离子同时在多孔电极中传输。2024年的研究表明，通过优化气体扩散层的孔隙率梯度设计（从催化剂层的30%逐渐增加到流场板的70%），可以将水淹临界电流密度提高35%。

更前沿的是阴离子交换膜（AEM）电解槽的仿真。与PEM不同，AEM使用非贵金属催化剂，但面临CO₂毒化问题。2024年的多物理场模型显示，在电解槽入口添加微量的KOH可以形成”pH缓冲层”，将CO₂的传质阻力提高10倍，从而保护催化剂。

3. 反应-扩散派：当化学遇上传输

很多传质过程伴随着化学反应，比如CO₂被胺溶液吸收、药物从聚合物载体中释放等。这时需要在传质方程中加入反应源项 RRR：R=kcn或R=k(ceq−c)R = k c^n \quad \text{或} \quad R = k(c_{eq} – c)R=kcn或R=k(ceq​−c)

2024热门应用：碳捕集的”分子陷阱”

全球每年排放超过360亿吨CO₂，而碳捕集技术（CCUS）被视为脱碳的关键。2024-2025年，有限元仿真在碳捕集领域的应用呈现爆发式增长：

  • 胺吸收塔优化：使用速率基模型（Rate-based Model）代替传统的平衡级模型，可以更准确地预测传质系数。研究显示，DEA（二乙醇胺）在生物气CO₂捕集中的效率比MDEA高15%。
  • 中空纤维膜接触器（HFMC）：这种”把气体和液体用膜隔开”的设备，传质面积可以达到传统填料塔的10倍。2024年的CFD-有限元耦合模型发现，逆流配置比并流配置的CO₂吸收效率高20-30%，因为逆流保持了更大的浓度驱动力。
  • 化学链燃烧：一种新兴的零碳燃烧技术，通过金属氧化物颗粒（如Fe₂O₃）作为”氧载体”循环传递氧。2024年的多尺度模型（从颗粒尺度的DFT计算到反应器尺度的CFD）显示，添加5%的Zr掺杂可以将CaO基吸附剂的CO₂吸附容量提高40%。

2025年的前沿：AI+多物理场传质

传质仿真正在经历一场”智能化革命”。

物理信息神经网络（PINNs）

传统的有限元方法需要精细的网格划分，对于复杂几何（如多孔介质的真实CT扫描结构）计算成本极高。2024年兴起的**物理信息神经网络（PINNs）和物理信息Kolmogorov-Arnold网络（PIKANs）**提供了一种新思路：

  • 将传质方程（如对流-扩散方程）作为神经网络的”损失函数”约束
  • 可以在无网格的情况下求解偏微分方程
  • 对于高维参数空间（如多孔介质的随机孔隙结构）特别有效

在地下能源储存（如CO₂地质封存、氢能地下储库）的多尺度模拟中，PINNs可以将计算速度提高10-100倍。

机器学习辅助的药物控释设计

2024年发表的一项研究将传质仿真与机器学习结合，用于优化多孔聚合物载体的药物释放曲线。研究团队使用有限元方法模拟药物在载体中的扩散-溶解过程，然后用梯度提升回归（Gradient Boosting）模型建立”结构-释放性能”的代理模型。结果显示，AI模型的预测精度（R²=0.9977）足以替代昂贵的实验筛选，将新药载体的开发周期从6个月缩短至2周。

实用指南：如何选择你的传质仿真工具？

应用场景推荐工具关键功能
锂电池/燃料电池COMSOL Multiphysics电池模块、三次电流分布、多孔电极
化工反应器/碳捕集ANSYS Fluent + 自定义标量输运多相流、反应动力学、膜分离
木材干燥/食品工程COMSOL 或 自定义FEM代码热-湿耦合、各向异性扩散、变形-传质耦合
氢能储罐（液氢/金属氢化物）Fluent + UDF 或 OpenFOAM相变传质、低温热力学、多孔介质非平衡模型
药物控释/生物材料COMSOL + MATLAB/Python AI工具箱多孔介质扩散、降解动力学、代理模型优化

结语：从咖啡杯到碳中和

传质仿真看似高深，实则根植于日常生活。当你下次冲泡咖啡时，不妨想想：这杯咖啡的萃取曲线，与价值千万的氢燃料电池水管理模型，本质上都在求解同一个对流-扩散方程。

在2025年，随着AI for Science的兴起和多物理场耦合能力的增强，有限元传质仿真正在突破传统工程边界。无论是为了实现碳中和的CCUS技术，还是为了下一代固态电池的离子传导优化，传质仿真都将是不可或缺的”数字显微镜”。

毕竟，在这个分子不断运动的世界里，理解传质，就是理解变化本身。

参考文献索引：

  • Wang & Yang, BioResources 2025 – 木材干燥有限元技术综述
  • ResearchGate 2025 – 电化学系统仿真软件比较
  • Nottingham大学 – PEM燃料电池三维多相流模型
  • SciOpen 2025 – 地下能源储存多尺度建模综述
  • COMSOL官方 – 燃料电池与电解槽模块功能
  • MDPI Energies 2025 – 液氢储罐传热传质数值研究
  • Int. J. Hydrogen Energy 2025 – 金属氢化物储氢系统CFD模拟
  • Springer 2025 – 生物气CO₂捕集胺溶剂优化
  • Research Square 2024 – 中空纤维膜接触器传质模拟
  • Sci Rep 2024 – 药物控释传质与AI建模

本文撰写于2025年，结合了最新的学术研究动态与工业应用趋势。

仿真工程师必懂：偏导、梯度、散度、旋度、拉普拉斯｜生活例子+标准公式+COMSOL案例一篇打通

发表评论

（有趣不晦涩、公式不吓人、看完能分清、建模用得上）

做有限元、做多物理场耦合，偏导、梯度、散度、旋度、拉普拉斯这五个词天天见。 满屏的 ∂\partial∂、∇\nabla∇、∇⋅\nabla\cdot∇⋅、∇×\nabla\times∇×、Δ\DeltaΔ，到底在说啥？ 它们不是玄学，而是描述世界如何变化的语言： 热怎么传、风怎么吹、电怎么跑、水怎么旋、结构怎么平衡，全靠它们。 这一篇把趣味生活例子 + 标准LaTeX公式 + 工程意义 + COMSOL真实案例揉在一起， 让你记得住、分得清、用得上。

0）总纲：五句话先把它们“翻译成人话”

  • 偏导数：只看某一个方向的变化快慢
  • 梯度：哪条路最陡、变化最快（场的驱动力）
  • 散度：这里是喷出来（源）还是吸进去（汇）
  • 旋度：这里有没有打转、漩涡、旋转
  • 拉普拉斯：场是凸是凹，能不能慢慢变平稳、达到平衡

1）偏导数 Partial Derivative

一句话理解

只盯一个方向看变化，其他方向暂时“冻结”。

标准公式（三维标量场 u(x,y,z)u(x,y,z)u(x,y,z)）

∂u∂x,∂u∂y,∂u∂z\frac{\partial u}{\partial x},\quad \frac{\partial u}{\partial y},\quad \frac{\partial u}{\partial z}

生活/生产例子

  • 火锅：只关心左右温度差多少
  • 电池散热：只看厚度方向温升快慢
  • 芯片：只看垂直基板方向热流变化

仿真里的作用

所有斜率、方向导数、后处理里的“某方向导数”，底层都是偏导。

COMSOL表达式

d(T,x)、d(phi,y)

2）梯度 Gradient ∇u

一句话理解

标量场变化最陡的方向 + 最大变化率。

梯度 = 场的“驱动力”。

标准公式

∇u=(∂u∂x, ∂u∂y, ∂u∂z)\nabla u = \left( \frac{\partial u}{\partial x},\ \frac{\partial u}{\partial y},\ \frac{\partial u}{\partial z} \right)

生活/生产例子

  • 冬天窗户：热量沿着温度梯度往外跑
  • 电流：沿着电势梯度流动
  • 水流：沿着压力梯度流动

没有梯度，就没有传热、没有电流、没有流动。

COMSOL官方案例：磁场梯度（粒子 / MRI / 磁悬浮）

  • 用途：粒子偏转、磁悬浮、MRI磁场均匀性分析
  • 核心：梯度越大，场变化越剧烈，受力/效应越强

3）散度 Divergence ∇⋅F

一句话理解

向量场在这里是“喷泉”还是“吸尘器”。

散度 = 源 / 汇 / 守恒。

标准公式

∇⋅F=∂Fx∂x+∂Fy∂y+∂Fz∂z\nabla\cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}

生活/生产例子

  • 吹风机出风口：散度 > 0（源）
  • 吸尘器进风口：散度 < 0（汇）
  • 水管中间一段：不增不减 → 散度 = 0

工程核心方程

不可压缩流体（水、油、低速风）：∇⋅u=0\nabla\cdot \mathbf{u} = 0

这就是CFD里最核心的质量守恒。

COMSOL官方案例：后台阶流动（汽车尾流 / 风道）

  • 典型CFD基准算例
  • 核心约束：速度散度=0，保证流体体积守恒

4）旋度 Curl ∇×F

一句话理解

场在这里“转不转”、“涡不涡”。

标准公式

∇×F=∣exeyez∂∂x∂∂y∂∂zFxFyFz∣\nabla\times \mathbf{F} = \begin{vmatrix} \mathbf{e}_x & \mathbf{e}_y & \mathbf{e}_z \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_x & F_y & F_z \end{vmatrix}

展开分量形式：(∂Fz∂y−∂Fy∂z, ∂Fx∂z−∂Fz∂x, ∂Fy∂x−∂Fx∂y)\left( \frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z},\ \frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x},\ \frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y} \right)

生活/生产例子

  • 马桶放水、台风、咖啡搅拌：旋度≠0
  • 静电场、重力场：直线指向，不旋转 → 旋度=0

工程最经典：电磁炉 / 感应加热

法拉第电磁感应定律（全靠旋度吃饭）：∇×E=−∂B∂t\nabla\times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}

交变磁场 → 电场旋度≠0 → 金属内部产生涡流 → 发热

COMSOL官方案例：感应加热（金属熔炼 / 淬火）

  • 工业热处理、焊接、熔炼核心模型
  • 直接求解旋度方程

5）拉普拉斯算子 Laplacian Δu=∇2u

一句话理解

描述场的“凹凸/弯曲程度”，负责让场变平稳、达到平衡。

标准公式

Δu=∇⋅(∇u)=∂2u∂x2+∂2u∂y2+∂2u∂z2\Delta u = \nabla\cdot(\nabla u) = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}

生活/生产例子

  • 一杯热水放凉，最后温度均匀：趋向 ΔT=0
  • 房间恒温、静电平衡、结构静力变形稳定：都满足拉普拉斯类方程

工程最常用方程

  • 拉普拉斯方程（无源、稳态、平衡）：

Δu=0\Delta u = 0

  • 泊松方程（有源、有热源/电荷/载荷）：

Δu=f\Delta u = f

覆盖几乎所有静场/稳态问题：

稳态热传导、静电场、地下水渗流、结构静力、物质扩散

COMSOL官方案例：点源泊松方程（点热源 / 点电荷 / 集中力）

  • 芯片热点、针状电极、集中载荷、裂纹尖端
  • 最经典的“场的平衡与扩散”模型

6）一张表彻底分清：5个核心算子对比

名称数学符号核心公式简记作用对象输出人话核心
偏导数∂u∂x\dfrac{\partial u}{\partial x}∂x∂u​单方向求导标量标量某方向变化快慢
梯度∇u\nabla u∇u(∂x,∂y,∂z)u(\partial_x,\partial_y,\partial_z)u(∂x​,∂y​,∂z​)u标量向量最陡方向、驱动力
散度∇⋅F\nabla\cdot\mathbf{F}∇⋅F∂xFx+∂yFy+∂zFz\partial_x F_x+\partial_y F_y+\partial_z F_z∂x​Fx​+∂y​Fy​+∂z​Fz​向量标量源/汇、守恒
旋度∇×F\nabla\times\mathbf{F}∇×F叉乘行列式向量向量旋转、涡流
拉普拉斯Δu=∇2u\Delta u=\nabla^2 uΔu=∇2u∂x2+∂y2+∂z2\partial_x^2+\partial_y^2+\partial_z^2∂x2​+∂y2​+∂z2​标量标量平衡、扩散、稳态

7）仿真工程师最该记住的4句物理

  1. 梯度负责“驱动”：温差、电势差、压力差 → 推动一切流动与传递
  2. 散度负责“守恒”：流体不增不减、电荷守恒、质量守恒
  3. 旋度负责“旋转与感应”：涡流、电机、感应加热全靠它
  4. 拉普拉斯负责“平衡与稳态”：静场、稳态、扩散问题的核心骨架

你在 COMSOL 里选的每一个物理场接口：

传热、CFD、静电、磁场、结构、扩散

背后都是这五个算子在支撑。

🌈 光学仿真的”三重宇宙”：从纳米到宏观的数值探险

发表评论

“光是一种电磁波，但在不同尺度下，它有时是粒子，有时是射线，有时是复杂的矢量场——这取决于你问的是哪位数值方法专家。”

光学仿真领域就像一个被分割成多个平行宇宙的奇幻世界。在这个世界里，同一束光在纳米尺度是复杂的电磁场振荡，在微米尺度是优雅的波动传播，而在宏观尺度则简化为笔直的光线。今天，我们将穿越这三个”宇宙”，探索各自的仿真”方言”、软件工具，以及那些必读的经典”圣经”。

🔬 第一宇宙：亚波长尺度（< λ）——”麦克斯韦的微观世界”

当你凝视一个比光波长还小的纳米颗粒时，你看到的不是简单的阴影，而是等离子体共振、近场增强和光子局域化的奇幻景象。在这里，麦克斯韦方程组是绝对的统治者，没有任何近似可以逃脱它的法眼。

🛠️ 核心武器库

方法原理超能力致命弱点
FDTD (时域有限差分)在Yee网格上直接离散麦克斯韦方程宽带响应一次搞定；适合复杂材料内存杀手；曲面几何需要亚像素平滑
FEM (有限元法)变分原理+非结构化网格复杂几何适应性极强；自适应网格大规模问题矩阵求解慢；周期性结构内存爆炸
FMM/RCWA (傅里叶模态法)平面波展开+散射矩阵周期性光栅的”闪电侠”；超表面设计首选非周期结构直接”死机”
BEM (边界元法)仅离散界面+格林函数降维打击（3D→2D）；开放边界天然处理稠密矩阵；多尺度问题头疼

💻 软件装备指南

商业神器（氪金玩家首选）：

  • Ansys Lumerical FDTD 🏆 光子学仿真的”瑞士军刀”，内置FDTD、FEM（FEEM）、时域和频域模式求解器。2024 R1版本甚至加入了量子计算和AR/VR仿真模块 。其DGTD（间断伽辽金时域）求解器适合多物理场耦合。
  • COMSOL Multiphysics 🧩 多物理场仿真的”乐高积木”，Ray Optics和Wave Optics模块无缝衔接。特别适合光-热-力耦合问题，比如激光加热或光声效应。
  • Synopsys RSoft Photonic Device Tools 📡 专注光子器件，包含：
    • BeamPROP：光束传播法（BPM），模拟波导器件
    • FullWAVE：FDTD求解器，处理纳米结构
    • DiffractMOD：RCWA求解器，光栅分析
    • FemSIM：FEM模式求解器
  • JCMsuite 🔬（德国JCMwave GmbH） 基于有限元的高精度求解器，专长于光子晶体、波导、光伏器件和纳米结构仿真，支持自适应网格和高阶元

开源宝藏（极客精神）：

  • Meep 🐍（MIT出品，GPL v3+） 学术界最著名的开源FDTD软件，由Steven G. Johnson、John D. Joannopoulos和Marin Soljačić团队开发。支持C++/Python/Scheme接口，MPI并行，内置亚像素平滑、非线性材料和伴随求解器（用于拓扑优化）。其2010年发表在Computer Physics Communications的论文已成为纳米光子学研究的”标配”引用（超过1000次）
  • gprMax ⛏️（爱丁堡大学，GPL v3+） 专为探地雷达设计的FDTD软件，但通用性极强：
    • v1/v2（1996-）：Antonis Giannopoulos开发，基于Matlab
    • v3+（2015-）：Craig Warren重构，完全Python化，支持CUDA GPU加速和OpenMP并行
  • OpenEMS 🔓（德国杜伊斯堡-埃森大学，GPL v3+） 由Thorsten Liebig于2010年在ATE实验室（General and Theoretical Electrical Engineering）开发。支持EC-FDTD（共形FDTD）、圆柱坐标系，Matlab/Octave和Python双接口

📚 必读圣经

  1. 《Computational Electrodynamics: The Finite-Difference Time-Domain Method》 (第三版, 2005) Allen Taflove & Susan C. Hagness 出版社：Artech House ISBN：978-1580538329 地位：FDTD领域的”圣经”，超过1000页的鸿篇巨著。从Yee算法到色散材料，从PML边界到近远场变换，无所不包。Taflove教授（西北大学）被誉为FDTD方法的”教皇”
  2. 《Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology》 (2013) Allen Taflove, Ardavan Oskooi & Steven G. Johnson 亮点：涵盖光子晶体、等离子体、光力计算等前沿，Meep的主要开发者Oskooi参与撰写
  3. 《The Finite Element Method in Electromagnetics》 (第三版, 2014) Jian-Ming Jin (金建铭) 出版社：Wiley-IEEE Press ISBN：978-1118571361 地位：电磁FEM的权威教材，作者为伊利诺伊大学厄巴纳-香槟分校教授。从静电学到天线辐射，从频域到时域，系统全面。适合想深入理解FEM数学基础的读者

关键学术论文：

  • Oskooi et al. (2010). “MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method”. Computer Physics Communications, 181(3), 687-702. DOI: 10.1016/j.cpc.2009.11.008
  • Warren et al. (2016). “gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar”. Computer Physics Communications. DOI: 10.1016/j.cpc.2016.08.020

🌊 第二宇宙：介观尺度（~ λ）——”波动光学的舞蹈”

当结构尺寸与波长相当（几微米到几十微米），光开始展现它优雅而复杂的波动本性。衍射、干涉、矢量效应——这里既不是简单的几何光学，也不是纯粹的近场电磁学，而是两者的”量子纠缠”。

🎭 特色方法

1. 波束包络法 (Beam Envelopes) 想象光场是一个”慢变包络”乘以一个”快变载波”：E=Eslow⋅e−jk⋅r\mathbf{E} = \mathbf{E}_{slow} \cdot e^{-j\mathbf{k}\cdot\mathbf{r}}E=Eslow​⋅e−jk⋅r。这样网格只需解析包络，密度降低10倍！适合光纤、透镜和定向传播系统。

2. 模式匹配法 / EME (Eigenmode Expansion) 将器件切成”薄饼”状的均匀层，每层求解本征模，通过散射矩阵连接。对于硅光波导和光栅耦合器，这是速度与精度的完美平衡。

3. 物理光学法 (Physical Optics) 基于Stratton-Chu积分，从表面电流计算远场。是连接全波与几何光学的”虫洞”。

💻 软件装备指南

  • COMSOL Wave Optics Module 束包络法的工业级实现，支持双向耦合和Floquet周期性边界，是光纤器件仿真的首选。
  • Lumerical MODE 2.5D FDTD和EME求解器，专门优化硅光子和集成光学设计。
  • VirtualLab Fusion（德国LightTrans） 由Jena大学Frank Wyrowski教授团队开发，采用独特的场追迹（Field Tracing）技术，自动在几何光学和波动光学间切换。专长于激光系统、衍射光学元件（DOE）、自由曲面和AR/VR设计
  • JCMsuite 在微米尺度同样表现出色，特别是波导模式分析和光纤耦合仿真

📚 必读圣经

  1. 《Principles of Optics》 (第七版扩展版, 1999/2019) Max Born & Emil Wolf 出版社：Cambridge University Press 地位：光学领域的”广义相对论”，从电磁理论到衍射、干涉、晶体光学，数学严谨性无与伦比。2019年60周年纪念版（纪念1959年第一版）新增CAT扫描、散射层析等内容，由四位诺贝尔奖得主（Steven Chu, Stefan Hell, William Phillips, Donna Strickland）联名推荐
  2. 《Numerical Simulation of Optical Wave Propagation with Examples in MATLAB》 (2010) Jason D. Schmidt 出版社：SPIE Press ISBN：978-0819483263 实用度：★★★★★ 专注波动光学仿真，涵盖角谱法、分步傅里叶方法，附MATLAB代码，适合大气光学和自适应光学研究
  3. 《Photonics: Optical Electronics in Modern Communications》 (2006) Amnon Yariv & Pochi Yeh 出版社：Oxford University Press 现代光电子学的经典教材，从波导模式到非线性光学，系统而深入

🎯 第三宇宙：宏观尺度（>> λ）——”几何光学的回归”

当结构尺寸远大于波长（>100λ），光终于”疲惫”了，波动性退居幕后，射线近似成为主导。在这里，光沿直线传播，遵循反射定律和斯涅尔定律，就像古希腊人想象的那样——只不过我们现在有了蒙特卡洛和优化算法。

🚀 核心武器

方法原理适用场景
光线追踪 (Ray Tracing)求解Eikonal方程，追踪光线路径成像系统、照明设计、AR/VR光波导
光束追踪 (Beam Tracing)追踪高斯光束而非无限细光线激光谐振腔、光纤耦合
一致性绕射理论 (UTD/GTD)几何光学+边缘绕射修正天线罩、复杂边界散射

💻 软件装备指南

成像设计三巨头：

  • Zemax OpticStudio 👑 光学设计的”Photoshop”，Sequential和Non-Sequential双模式，优化算法强大，全球光学工程师的”母语”
  • Code V 🛡️ Synopsys出品，航空航天和国防领域的”贵族”，以公差分析和像差控制著称
  • OSLO 🎓 Lambda Research出品，教育版免费，适合学术入门

照明与杂光分析：

  • LightTools 💡 Synopsys的照明设计利器，支持自由曲面优化、杂光分析和生物视觉仿真（如眩光分析）。与CODE V无缝集成，是汽车照明和显示背光的行业标准
  • TracePro 🔍 CAD-like界面，擅长杂散光和热辐射分析，适合航天器和精密仪器
  • FRED 🌈（Photon Engineering） 通用非序列光线追踪，支持偏振和散射建模。FREDmpc版本支持GPU加速，可处理数千万条光线

新兴力量：

  • 3DOptix ☁️ 云端光学仿真，拖拽式界面，适合远程协作和教育
  • Ansys Speos 🚗 专注人眼视觉和汽车照明，支持HUD和AR-HUD设计

📚 必读圣经

  1. 《Optical System Design》 (2000) Robert E. Fischer, Biljana Tadic-Galeb, Paul R. Yoder 出版社：McGraw-Hill 从像差理论到公差分析，系统设计全流程指南
  2. 《Illumination Engineering: Design with Nonimaging Optics》 (2013) R. John Koshel 出版社：Wiley-IEEE Press 非成像光学（如太阳能聚光器、LED准直器）的权威教材
  3. 《Handbook of Optics》 (第三版, 2009) Michael Bass (Editor) 出版社：McGraw-Hill 光学工程师的”百科全书”，涵盖设计、制造、测试全链条

🌉 跨宇宙旅行：多尺度耦合的艺术

现实世界的光学系统往往横跨多个尺度。比如一个AR眼镜：

  • 纳米尺度：衍射光栅的亚波长结构（FDTD）
  • 微米尺度：光波导的模式传播（EME）
  • 宏观尺度：人眼看到的最终图像（Ray Tracing）

🔗 混合策略

  1. 顺序耦合：FDTD提取光栅的相位函数 → 导入Zemax作为自定义面型
  2. 代理模型：用FDTD生成数据集，训练神经网络替代耗时仿真
  3. 域分解：FEM处理纳米区域，射线追踪处理远场，通过惠更斯面耦合

💻 跨尺度神器

  • VirtualLab Fusion：唯一真正实现场追迹（Field Tracing）的商业软件，自动在几何和波动光学间切换
  • Lumerical + Zemax / Speos：Ansys生态内的数据链路，支持从纳米到系统的全流程

🎓 给初学者的”升级路线图”

Level 1 (本科生/入门):
  └─ 读 Born & Wolf《Principles of Optics》→ 玩 OSLO / 3DOptix
  └─ 理解光线追踪和基本像差

Level 2 (研究生/进阶):
  └─ 读 Taflove《Computational Electrodynamics》→ 装 Meep / Lumerical FDTD
  └─ 掌握 FDTD 和波导模式分析
  └─ 精读 Oskooi et al. (2010) CPC论文

Level 3 (博士/专家):
  └─ 读 Jin《FEM in Electromagnetics》(2014) → 用 COMSOL / JCMsuite
  └─ 研究多尺度耦合和拓扑优化

Level 4 (大师):
  └─ 开发自己的求解器，发表像 Oskooi & Johnson 那样的 CPC 论文

📖 终极书单（按尺度分类）

尺度经典教材数值方法软件手册
亚波长Jackson《Classical Electrodynamics》Taflove & Hagness (2005), ISBN 978-1580538329Meep Documentation
介观Born & Wolf《Principles of Optics》(2019纪念版)Schmidt (2010), ISBN 978-0819483263COMSOL Wave Optics User Guide
宏观Hecht《Optics》Koshel《Illumination Engineering》Zemax Knowledge Base

必读论文清单：

  1. Oskooi, A. F., et al. (2010). “MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method”. Computer Physics Communications, 181(3), 687-702. DOI: 10.1016/j.cpc.2009.11.008
  2. Warren, C., et al. (2016). “gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar”. Computer Physics Communications. DOI: 10.1016/j.cpc.2016.08.020

🌟 结语：选择你的”宇宙”

光学仿真的魅力在于，没有最好的方法，只有最合适的方法。当你面对一个包含纳米光栅、微米波导和宏观透镜的AR系统时，不要试图用一个FDTD网格吞下整个宇宙——那会让你的工作站”壮烈牺牲”。相反，学会在不同尺度间”穿梭”，用FDTD捕捉等离子体共振，用EME计算波导耦合，用Ray Tracing预测人眼所见。

正如费曼所说：”自然界并不在乎我们的数学困难，她只是继续她的演化。” 我们的任务，是选择正确的数值”镜头”，去窥探她的秘密。

Happy Simulating! 🚀✨

参考文献索引

软件与工具：

  • Gitnux (2026). “10 Best Optical Simulation Software For 2026”
  • Meep Documentation. Read the Docs
  • Synopsys. “LightTools Features”
  • OPDO.ai (2025). “Optical Simulation Software: A Complete Guide”
  • 驱动网 (2024). “ANSYS Lumerical 2024 R1新功能”
  • LightTrans. “VirtualLab Fusion Product Page”
  • PhotonicsViews (2012). “VirtualLab Fusion”
  • SPIE (2012). “Fast physical optics” by Frank Wyrowski
  • gprMax Documentation. “Introduction to gprMax”
  • Synopsys. “RSoft Photonic Device Tools”
  • Warren et al. (2016). “gprMax” CPC paper
  • Synopsys. “RSoft FullWAVE”
  • Giannopoulos (2005). “Modelling ground penetrating radar”
  • Oskooi et al. (2010). “MEEP” CPC paper
  • Photon Engineering. “FRED Optical Engineering Software”
  • Google Scholar. “MEEP” citations
  • Photon Engineering. “FREDmpc GPU-Accelerated Ray Tracing”
  • OpenEMS Documentation. “Introduction”
  • OpenEMS Forum. “About the OpenEMS category”
  • JCMwave/JCMsuite Product Information

经典教材：

  • Born, M. & Wolf, E. (2019). Principles of Optics 60th Anniversary Edition. Cambridge University Press.
  • Jin, J.-M. (2014). The Finite Element Method in Electromagnetics (3rd ed.). Wiley-IEEE Press. ISBN 978-1118571361.
  • Yariv, A. & Yeh, P. (2006). Photonics: Optical Electronics in Modern Communications. Oxford University Press.
  • Open Library. “The finite element method in electromagnetics” (2014 edition)
  • Taflove, A., Oskooi, A., & Johnson, S. G. (2013). Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology. Artech House.
  • Schmidt, J. D. (2010). Numerical Simulation of Optical Wave Propagation with Examples in MATLAB. SPIE Press. ISBN 978-0819483263.
  • Amazon. “Computational Electrodynamics: The Finite-Difference Time-Domain Method” (2005 edition)
  • Open Library. “Computational electrodynamics” (2005 edition)
  • Google Books. “Computational Electrodynamics” (2005 edition)
  • Amazon. “The Finite Element Method in Electromagnetics” (2014 edition)

振动世界的三重密码：模态、响应谱与随机振动的”3σ法则”

发表评论

瓜哥

“当你在桥上奔跑，在车里颠簸，在摩天大楼里感受微风——你都在经历振动的三重境界。”

第一重境界：模态数据——结构的”指纹与嗓音”

什么是模态？

想象你正在面试一位歌手。你不需要听他唱完整首歌，只需要让他发出几个特定的音阶（do、re、mi…），你就能判断他的音域、音色和肺活量。

模态分析就是给结构做的”发声测试”。

每个结构都有自己的固有频率（Natural Frequency）——就像人的嗓音有高低之分。当外部激励的频率与结构的固有频率重合时，就会发生共振，这时候结构会”唱”得特别大声（振幅巨大），甚至”破音”（损坏）。

模态数据的三个核心参数

参数物理意义生活比喻
固有频率 (Hz)结构自由振动的频率歌手能发出的最低音到最高音
振型 (Mode Shape)结构在各频率下的变形形态唱歌时身体的哪个部位在用力（胸腔共鸣vs头腔共鸣）
阻尼比 (Damping Ratio)振动能量衰减的快慢歌手唱完一个音后，声音多久消失

有趣的事实：1940年塔科马海峡大桥坍塌，就是因为风吹出的卡门涡街频率（约0.2Hz）刚好撞上了桥梁的扭转模态频率。风没多大，但桥”唱”得太投入，把自己唱断了。

模态分析告诉我们：结构不是”死”的，它们时刻准备着以特定的方式”跳舞”。

第二重境界：响应谱分析——地震的”体检报告”

从时域到频域的魔法

假设地震来了，地面像疯了一样乱抖。你想知道家里的书架会不会倒，但盯着那团混乱的加速度曲线（时域信号），你什么都看不出来。

这时候，工程师祭出了响应谱（Response Spectrum）这个大杀器。

什么是响应谱？

响应谱不是描述地震本身，而是描述**”地震对一系列不同周期的单自由度系统的影响”**。

想象一排摆长不同的秋千（周期不同），同时遭受同样的地面晃动。有的秋千会剧烈摆动（共振），有的几乎不动。响应谱就是记录每个秋千最大摆幅的曲线。

为什么用响应谱？

因为它把混乱的地震变成了设计图纸上的标尺！

工程师不需要知道地震的每一秒在干什么，只需要查表：

  • 我的结构第一阶周期是0.5秒 → 查谱得加速度0.4g → 计算内力
  • 第二阶周期是0.2秒 → 查谱得加速度0.6g → 计算内力

这就像看体检报告：不需要看懂血液里每个红细胞在干嘛，只需要看”白细胞计数偏高”这个结论。

响应谱的类型

类型含义应用场景
加速度响应谱各周期下的最大加速度计算惯性力，结构强度设计
速度响应谱各周期下的最大速度评估设备功能失效
位移响应谱各周期下的最大位移检查碰撞、间隙问题

响应谱是地震工程师的”作弊码”——把不可预测的混乱，变成了可查询的表格。

第三重境界：随机振动与”3σ法则”——概率世界的生存指南

当振动不再是”确定”的

地震来了，你知道它会发生，但不知道具体哪一秒会抖多厉害。飞机在天上飞，你知道会遇到湍流，但不知道具体哪个时刻会颠簸。

这就是随机振动（Random Vibration）——用概率统计描述的不确定性世界。

功率谱密度（PSD）：振动的”指纹图谱”

随机振动不用时间-加速度曲线描述，而是用功率谱密度（PSD, Power Spectral Density），单位通常是g²/Hz。

PSD就像音乐的频谱图：

  • 低音鼓点 → 低频高能量
  • 小提琴 → 高频低能量
  • 整体看，你知道每个频段有多少”能量”，但不知道具体节奏

3σ法则：工程界的”保守主义浪漫”

这是本文最精彩的部分，也是最容易被误解的地方。

在随机振动分析中，Abaqus等软件会输出RMS值（均方根，1σ），但工程师报告时常常乘以3，得到3σ值。

为什么是3倍？

因为对于正态分布（高斯分布）：

  • ±1σ 范围内包含 68.3% 的概率
  • ±2σ 范围内包含 95.4% 的概率
  • ±3σ 范围内包含 99.7% 的概率
正态分布3σ

工程解释：

“我们假设结构在99.7%的时间内，应力/位移都不会超过这个3σ值。剩下0.3%？那是上帝的领域，我们不管了。”

3σ位移 vs 3σ应力的物理意义

指标含义工程应用
3σ位移99.7%概率下不会超过的变形量检查间隙、碰撞、安装空间
3σ应力99.7%概率下不会超过的应力水平强度校核、疲劳寿命预估

关键理解：

  • 3σ不是最大值！ 理论上随机振动的最大值可以无限大（只是概率极低）。
  • 3σ是一个统计边界，表示”几乎肯定不会超过”的阈值。
  • 如果你看到3σ应力超过了屈服强度，意味着有0.3%的概率会发生塑性变形——对于卫星发射这种一次性事件，通常可接受；对于每天运行的汽车，可能不行。

一个有趣的思维实验

假设你设计了一个航天器支架，随机振动分析显示：

  • 1σ应力 = 100 MPa
  • 3σ应力 = 300 MPa
  • 材料屈服强度 = 280 MPa

问题：这个设计安全吗？

答案：看情况！

  • 如果这是价值10亿美元的卫星，且发射窗口一年只有一次 → 不安全（有0.3%概率失败，期望损失30万美元）
  • 如果这是批量生产的无人机，且可以维修 → 可接受（99.7%的存活率，经济效益可覆盖风险）

这就是工程的艺术：3σ是数字，决策是哲学。

三重境界的对比与联系

特性模态分析响应谱分析随机振动分析
输入无（自由振动）设计地震谱PSD功率谱
输出频率、振型、阻尼最大响应包络值RMS值、3σ统计值
性质确定性确定性（包络）概率性
核心问题结构”会怎么唱”？结构”会被唱坏吗”？结构”唱坏的概率多大”？
比喻歌手体检歌手在特定歌曲下的表现歌手在随机点歌台上的长期表现

它们的关系：

模态分析（基础） → 提供频率、振型、阻尼
        ↓
响应谱分析（应用） → 利用模态叠加，求地震下的最大响应
        ↓
随机振动分析（进阶） → 利用模态叠加，求随机激励下的统计响应

给工程师的实用建议

1. 模态分析阶段

  • 不要只看频率，振型告诉你能量集中在哪（可能是薄弱环节）
  • 前6阶通常最重要（刚体模态除外），但复杂结构需要更多
  • 检查有效质量参与系数，确保90%以上质量被包含

2. 响应谱分析阶段

  • 方向组合要小心：SRSS（平方和开根）适合频率分离好的模态，CQC（完全二次组合）适合密集模态
  • 地震是随机的，响应谱是包络，结果偏保守，不要过度解读”精确值”

3. 随机振动分析阶段

  • 3σ是统计概念，不是物理极限，报告时要注明”基于高斯分布假设”
  • 疲劳分析需要更精细的循环计数（如雨流计数），不能直接用3σ应力
  • 注意单位：PSD是(g²/Hz)还是(m²/s⁴/Hz)，差着9.81²倍！

结语：振动分析的哲学

从模态到响应谱，再到随机振动，我们经历了从确定性到概率性的认知升级。

  • 模态告诉我们：结构有灵魂，它们以特定的方式呼吸
  • 响应谱告诉我们：灾难可以被量化，恐惧可以被表格驯服
  • 随机振动告诉我们：世界是不确定的，但不确定性本身可以被数学拥抱

3σ位移和应力，不是答案，而是一种承诺——

“我以99.7%的置信度向你保证，在设计的寿命内，在预期的环境下，这个结构不会背叛你的信任。”

剩下的0.3%？那是留给奇迹和意外的空间。毕竟，如果工程能100%预测一切，那还要保险做什么呢？

本文作者：一个相信”好的振动分析应该像好的故事——有结构、有冲突、有概率意义上的圆满结局”的工程师。

延伸阅读推荐：

  • Clough & Penzien《结构动力学》——振动分析的圣经
  • Abaqus Analysis User’s Guide 6.14——第6章关于随机振动的数学细节
  • 田石柱《结构随机振动》——中文世界的经典教材

希望这篇博文能帮你理解这三个概念！如果你需要针对某个具体部分（比如数学推导、Abaqus操作步骤）进行深化，我可以进一步补充。

在 COMSOL 中玩转自定义颜色：从十六进制到归一化色表的零代码工作流

发表评论

这是一篇保姆级教程，教你从零开始制作COMSOL 自定义颜色表（Color Table）。无需编程基础，只需浏览器和 Excel，就能將你在配色网站上心仪的渐变色（十六进制格式）转化为 COMSOL 可用的归一化 RGB 色表文件。

前言：为什么要自定义颜色表？

COMSOL 默认的 Rainbow（彩虹色）虽然醒目，但在学术出版中往往显得不够专业，且可能对色觉障碍读者不友好。通过自定义颜色表，你可以：

  • 使用 Viridis、Plasma 等感知均匀的色图（perceptually uniform colormaps）提升数据可读性
  • 匹配期刊品牌色或公司 VI 配色
  • 创建发散色图（diverging colormap）突出正负值变化

但 COMSOL 的色表文件要求 RGB 值在 0 到 1 之间（归一化），而设计网站上通常提供的是 十六进制代码（如 #1a5f7a）。本文将搭建这座桥梁。

准备工作：你需要什么？

  1. 浏览器：访问配色网站和在线转换工具
  2. Microsoft Excel（或 WPS、Google Sheets）：进行数据处理
  3. 记事本/Notepad++：生成最终的 .txt 文件
  4. 一段配色方案：从 Coolors.co、ColorBrewer 或 Adobe Color 挑选的十六进制色值

步骤一：获取十六进制颜色代码

首先，你需要一组按顺序排列的颜色（通常 5-10 个节点即可形成平滑渐变）。

推荐配色资源：

  • Coolors.co：生成器可导出 .csv，支持渐变色导出
  • ColorBrewer 2.0：专为数据可视化设计，提供色盲安全方案
  • Adobe Color：可提取图片主色调
  • Culori.js 或 Chroma.js 相关工具网站

示例：

假设我们创建一个从深蓝到浅青的渐变色图，收集到的十六进制代码如下：

提示：记下的顺序应该是从最小值到最大值（或从负到正）的渐变顺序。

步骤二：十六进制 → RGB 整数转换

十六进制代码（如 #ff5733）需要转换为三个 0-255 的整数（R、G、B）。

方法 A：使用在线批量转换工具（推荐）

打开浏览器，搜索 “Hex to RGB bulk converter” 或访问以下工具：

  • WebFX Color Converter：支持批量输入多行十六进制代码
  • W3Schools Colors Converter：逐个转换但非常可靠
  • codebeautify.org：可批量处理

操作流程：

  1. 在输入框中粘贴你的十六进制列表（每行一个，带 # 号或去掉均可）：
  1. 点击 “Convert” 或 “批量转换”
  2. 复制输出的 RGB 值（通常是 rgb(13, 27, 42) 格式或 CSV 格式）

方法 B：Excel 公式直转（无需外部工具）

如果你不想用在线工具，可以直接在 Excel 中解析十六进制：

假设十六进制 #0d1b2a 在 A1 单元格（去掉 # 号）：

列公式说明
R (B1)=HEX2DEC(LEFT(A1,2))提取前两位转为十进制
G (C1)=HEX2DEC(MID(A1,3,2))提取中间两位
B (D1)=HEX2DEC(RIGHT(A1,2))提取最后两位

注意：Excel 的 HEX2DEC 函数要求十六进制字符串不带 # 号。

步骤三：Excel 归一化处理（0-1 范围）

这是最关键的一步。COMSOL 要求颜色表中的 RGB 值必须是 0 到 1 之间的浮点数，而不是 0-255 的整数。

操作流程：

  1. 在 Excel 中建立工作表：
色节点HexR (0-255)G (0-255)B (0-255)R_normG_normB_norm
10d1b2a132742
21b3a4b275875
30064660100102

2.输入归一化公式： 在 R_norm 列（假设为 E2 单元格）输入：

3.向下填充： 选中公式单元格，双击右下角填充柄，自动计算所有行的归一化值。

4.格式化数值（重要）： COMSOL 支持小数点后 4-6 位精度即可。选中归一化列，设置单元格格式 → 数值 → 小数位数 4 或 5 位。

示例结果：

步骤四：生成 COMSOL 可用的 TXT 文件

COMSOL 的颜色表文件是纯文本，格式要求：

  • 每行三个数字，分别代表 R、G、B
  • 用空格分隔
  • 不要标题行
  • 不要用逗号分隔（除非是 .csv 后缀但 COMSOL 官方推荐 .txt）

操作流程：

  1. 在 Excel 中仅保留归一化列： 复制 R_norm、G_norm、B_norm 三列，选择性粘贴为数值到新区域（去除公式）。
  2. 组合数据（可选但推荐）： 如果 COMSOL 版本较旧，可能需要固定格式。可以直接复制三列到记事本，Tab 会被视为空格。
  3. 导入记事本： 打开记事本（Notepad）或 VS Code，粘贴数据。确保格式如下：
  1. 保存文件：
    • 文件名示例：my_cool_colormap.txt
    • 编码选择：UTF-8（默认即可）

步骤五：在 COMSOL 中导入并使用

  1. 在 COMSOL 中调用：
    • 添加一个二维/三维绘图组（如表面图）
    • 在颜色表设置（Color Table）中，最右侧有个导入按钮，点击
    • 选择刚保存的归一化颜色表txt文件名
    • 确保勾选平滑过渡（Smooth）以获得更柔和的渐变

进阶技巧：创建专业级色图

技巧 1：使用更多的节点

虽然 3-5 个颜色可以做简单渐变，但专业色图通常需要 7-15 个节点以避免色带（banding）。建议使用 Coolors 的 “Steps” 功能生成中间色。

技巧 2：创建发散色图（Diverging Colormap）

对于包含正负值的数据（如应力、压力差），建议对称地设置颜色：

  • 负值端：冷色（蓝）
  • 零值：中性色（白/灰）
  • 正值端：暖色（红）

在 Excel 中，确保归一化后的零值点物理上位于文件中间行。

技巧 3：颜色插值的一致性

COMSOL 默认会在你提供的节点间进行线性插值。如果你想严格控制某个颜色出现在特定的归一化位置（比如 0.5 处必须是白色），你需要在 Excel 中插入额外的行来固定该点。

技巧 4：透明度（Alpha）通道（高级）

从 COMSOL 5.5 版开始，支持 RGBA 格式（增加第四列 Alpha 透明度，0-1）。如需部分透明效果，可在 Excel 中添加第四列 Alpha_norm。

完整示例：海洋蓝到翡翠绿的渐变

原始十六进制（来自 ColorBrewer YlGnBu 调色板）：

Excel 中的转换过程：

HexRGBR_normG_normB_norm
ffffcc2552552041.00001.00000.8000
c7e9b41992331800.78040.91370.7059
7fcdbb1272051870.49800.80390.7333
41b6c4651821960.25490.71370.7686
1d91c0291451920.11370.56860.7529
225ea834941680.13330.36860.6588

最终的 ocean_emerald.txt：

将此文件保存到 COMSOL colors 目录后，你就可以在表面图中选择这个自定义色表，获得比默认 Rainbow 更适合展示温度或浓度场的配色。

常见问题解答（FAQ）

Q1：我可以直接用十六进制代码吗？ A：不可以。COMSOL 颜色表必须接受归一化的十进制 RGB 值（0-1）。

Q2：颜色顺序有什么讲究？ A：COMSOL 将第一行映射到 color range 的最小值，最后一行映射到最大值。确保你的颜色逻辑顺序与数据范围对应。

Q3：为什么我的色表显示为黑白色？ A：检查是否有归一化值超出了 0-1 范围（Excel 公式错误导致的大于 1 或负数）。COMSOL 会截断越界值，可能导致显示异常。

结语

掌握了这套”设计网站 → 在线转换 → Excel 归一化 → TXT 导出”的工作流，你就能像专业可视化设计师一样，为仿真结果匹配最合适的色彩语言。不再受限于默认的 Rainbow 色表，让科学数据以最清晰、最美观的方式呈现。

现在，打开配色网站，挑选一套你喜欢的渐变色，开始制作你的第一个 COMSOL 自定义色表吧！

关注公众号发送：COMSOL自定义颜色表 获得做好的excel文档

通过网盘分享的文件：COMSOL自定义颜色表处理.xlsx 链接: https://pan.baidu.com/s/1XkQc__MYKjuNqwpEOkBVpA?pwd=wjvd 提取码: wjvd

为什么大涡模拟（LES）如此”吃”计算资源？从湍流尺度到工程实践的深层解析

发表评论

在计算流体力学（CFD）领域，大涡模拟（Large Eddy Simulation, LES）常被视为”昂贵的精度”。它位于雷诺平均（RANS）和直接数值模拟（DNS）之间，既承诺了比RANS更丰富的湍流细节，又避免了DNS天文数字般的计算需求。然而，当工程师第一次尝试将RANS项目转向LES时，往往会被其数十倍甚至上百倍的计算成本**震惊。究竟是什么让LES如此消耗资源？

一、湍流能谱与”80%规则”：网格数量的指数级增长

LES的核心假设是：直接解析大尺度涡结构，只模型化小尺度涡（亚格子尺度）。但问题在于，什么是”大尺度”？

根据Kolmogorov能谱理论，LES需要解析至少80%的湍动能才能保证结果的可靠性。这意味着网格必须精细到足以捕捉积分长度尺度（Integral Length Scale），而不仅仅是宏观流动特征。

具体而言：

  • RANS：仅需捕捉几何特征和边界层厚度，网格数与雷诺数基本无关
  • LES：需要在积分尺度上布置至少5-10个网格单元
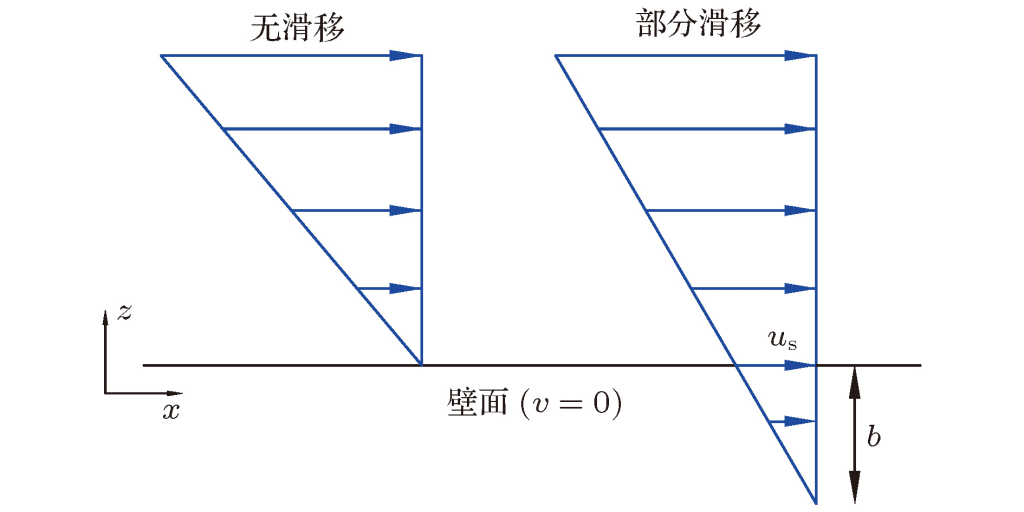
  • 壁面解析LES（WRLES）：在高雷诺数流动中，近壁区域的小尺度结构（条纹结构）尺寸正比于粘性长度尺度 lν=ν/uτl_\nu = \nu/u_\taulν​=ν/uτ​，导致网格数随雷诺数呈**~Re¹·⁹** 增长

举个例子：对于一个雷诺数Re=10⁶的航空外流问题，WRLES所需的网格数量可能达到数亿级别，而同等条件的RANS可能只需要几百万。

二、”壁面之殇”：近壁分辨率的沉重代价

壁面边界层是LES计算成本的最大瓶颈。在高雷诺数流动中，近壁区域的湍流结构具有以下特点：

  • 流向条纹结构（Streaks）的间距约为100个壁面单位（Δz⁺ ≈ 50-40）
  • 猝发事件的尺度极小，需要Δx⁺ ≈ 50-150，Δy⁺ < 1的网格分辨率

如果不使用壁面模型（Wall-Modeling），LES的分辨率要求几乎与DNS相当——网格点数正比于Re²。这使得壁面解析LES（WRLES）对于实际工程应用（如整机飞机或船舶）几乎不可行。

作为折中，壁面模型LES（WMLES） 通过在近壁区域使用雷诺平均或代数模型来放松网格要求，将成本降低到约**~Re¹·⁰**。但即便如此，其所需的网格量仍是RANS的10-100倍。

三、时间步长的”紧箍咒”：CFL条件与统计收敛

LES是三维非稳态计算，这带来了双重时间成本：

1. 瞬态时间步长的限制

为了准确捕捉涡的演化并保证数值稳定性，LES必须满足CFL条件（Courant-Friedrichs-Lewy）。通常要求CFL数小于1，理想情况下小于0.5。这意味着：

  • 对于边界层流动，时间步长可能需要小到 10⁻⁷秒 量级
  • 即使使用隐式时间推进，为了捕捉湍流的高频脉动，物理时间步长仍然受到声学尺度和**涡翻转时间（Eddy Turnover Time）**的限制

2. 统计收敛的漫长等待

与RANS可以收敛到稳态不同，LES必须在足够长的时间内进行模拟以获得统计稳态结果。通常需要10-20个流动穿越时间（Flow-through Time） 才能积累可靠的时均量和脉动量。

换算下来，一个LES案例可能需要计算数十万甚至上百万个时间步，而同等RANS可能只需数百次迭代。

四、数值格式的”精度陷阱”

LES对数值格式有极高的要求：

  • 低耗散（Low Dissipation）：高层迎风格式会抹平小尺度涡结构，需要中心差分或高精度重构（如WENO、Compact Scheme）
  • 低色散（Low Dispersion）：确保不同频率的波动以正确速度传播
  • 守恒性：动量守恒和动能守恒格式对LES尤为重要

这些高精度格式通常计算强度更大，且对网格质量（正交性、长宽比）要求严苛，进一步增加了前处理和计算成本。

五、工程实践中的妥协：WMLES与Hybrid方法

面对高昂的成本，工程界发展出了多种妥协方案：

方法网格数以Re为基准适用场景
DNS~Re²·⁷低雷诺数基础研究
WRLES~Re¹·⁹中等雷诺数学术验证
WMLES~Re¹·⁰高雷诺数工程应用
DES/IDDES~Re⁰·⁵-¹分离流、外流气动
RANS~Re⁰快速设计迭代

壁面模型LES（WMLES） 是目前高雷诺数工程应用的主流选择。它通过在距离壁面一定高度（通常是 y/δ≈0.1y/\delta \approx 0.1y/δ≈0.1）处施加应力边界条件，避免解析粘性底层，从而将网格需求降低一个数量级。

然而，WMLES引入了新的难题：对数层不匹配（Log-Layer Mismatch, LLM）。当网格在流向或展向过粗时，近壁速度剖面会出现系统性偏差，需要非常精细的Δx和Δz分辨率（即使y方向已使用壁面模型）。

结语：成本与精度的永恒博弈

LES的高计算成本根本源于湍流的多尺度特性。如果我们需要解析能量载涡（Energy-carrying Eddies）的动态行为，就必须在时间和空间上服从这些尺度的限制——而这些尺度在高雷诺数流动中往往是微米级和微秒级的。

随着计算机硬件的发展（尤其是GPU并行和自适应网格细化技术），LES正在从”学术研究工具”向”工程验证工具”转变。但就目前而言，在进行LES之前问自己两个问题：

  1. 流动是否包含RANS难以处理的大规模非定常分离或强涡脱落？
  2. 是否有足够的计算资源支持千万级网格和百万时间步的模拟？

如果答案都是肯定的，那么LES这把”昂贵的手术刀”将为你揭示湍流最精致的结构。

参考文献索引：

: 细说大涡模拟Large eddy simulation – 知乎专栏

: Grid requirements for wall-stress modeled LES – UMD : Turbulence modeling- Scales of turbulence lecture notes

: OpenAccess IYTE thesis on LES computational cost : Turbulence and CFD models lecture notes on DNS/LES costs

: Grid Resolution Requirements for Wall-Resolved LES – SJTU ISOPE 2024

: Wall Models for LES Based on Stanford Thesis : Wall-Modeled LES for Complex Flows – NIH/PMC

: 锥直型喷嘴内近壁处流动特性的大涡模拟 – 中国石油大学学报

力学仿真软件全景指南：从COMSOL到LS-DYNA，如何选择你的CAE利器？

发表评论

摘要： 面对COMSOL、ANSYS、ABAQUS、LS-DYNA等数十款CAE软件，工程师常陷入选择困难。本文摒弃简单的功能罗列，从多物理场、结构非线性、瞬态动力学、行业认证四大维度，为您梳理八款主流软件的核心生态位，并提供可直接落地的选型决策树。

一、软件江湖的”门派谱系”

在深入具体软件前，需理解CAE工具的底层分野逻辑：

  1. 按物理场广度：单物理场专业工具（如纯结构） vs 多物理场耦合平台（如电热磁流体固多场）
  2. 按非线性强度：线性分析（小变形、弹性材料） vs 非线性分析（接触、塑性、大变形）
  3. 按时间尺度：准静态（秒级以上） vs 瞬态动力学（毫秒以下，如碰撞爆炸）

基于以上维度，我们将八款软件划分为四大阵营：

阵营代表软件核心战场时间特征
多物理场平台COMSOL, ANSYS物理场耦合创新稳态/低频瞬态
结构非线性专家ABAQUS, Marc接触、塑性、材料失效准静态至中速
瞬态动力学霸主LS-DYNA, Radioss冲击、爆炸、跌落毫秒级显式
线性动力学权威NASTRAN振动、模态、气动弹性频域/稳态

二、多物理场阵营：从数学实验室到工程平台

1. COMSOL Multiphysics —— 多物理场之”王”

核心标签： PDE级开放、微纳尺度、科研创新

COMSOL的本质并非传统有限元软件，而是一个偏微分方程（PDE）求解平台。其最大特点是”方程级开放”——用户可直接访问底层控制方程，甚至输入自定义PDE。

独门绝技：

  • 真·多物理场耦合：支持电热磁流体固任意双向强耦合（如锂电池热失控与应力耦合、压电-热-结构三场交互），耦合深度远超ANSYS Workbench的数据传递模式
  • 微纳尺度权威：在MEMS器件、微流控芯片、固态电池微观结构模拟领域几乎是学术标准工具
  • App开发器：可将复杂模型封装为定制化仿真App，实现仿真能力的民主化

阿喀琉斯之踵：

  • 无显式动力学求解器：无法处理碰撞、爆炸等高速瞬态问题
  • 强结构非线性短板：大滑动接触、金属大变形塑性分析的收敛性和效率不如ABAQUS
  • 工业认证地位弱：航空结构适航认证、汽车碰撞安全报告目前不接受COMSOL结果

适用场景： 柔性电子皮肤设计、电池电化学-热-力耦合、MEMS多物理场优化、教学科研中的新物理现象探索。

2. ANSYS —— 工程多物理场之”相”

核心标签： Workbench集成、工业认证、易用性

ANSYS是多物理场领域的”工程实用主义者”，通过Workbench平台实现结构、流体（Fluent）、电磁（Maxwell）的深度集成。

独门绝技：

  • 流程自动化：几何修改后，结构、流体、热分析自动更新，适合设计迭代
  • 工业标准地位：在电子散热（芯片热管理）、旋转机械（叶轮机）等领域是事实标准
  • APDL参数化：强大的脚本语言支持复杂流程自动化

阿喀琉斯之踵：

  • 耦合深度有限：多物理场耦合多为单向或弱双向，强耦合（如电-化学-力）需手动干预
  • 非线性收敛性：处理复杂接触、大变形时稳定性不如ABAQUS，常需反复调整参数[^19][^26]

与COMSOL的抉择： 若做微纳尺度创新或需修改底层方程，选COMSOL；若做整车级热管理或电子散热工程验证，选ANSYS。

三、结构非线性阵营：接触与材料的”深水区”

3. ABAQUS —— 非线性分析之”霸”

核心标签： 接触算法、材料本构、工业级非线性

在非线性结构领域，ABAQUS是公认的”黄金标准”。其命名源于”Automatic But Accurate”，彰显其求解哲学。

独门绝技：

  • 接触算法之王：支持32种接触类型，自动处理过盈配合、大滑动摩擦等复杂工况，收敛稳定性业界最佳[^21]
  • 材料模型库：200+种本构模型，涵盖超弹性橡胶、混凝土损伤、复合材料层间失效、金属蠕变
  • 显式/隐式双求解器：Standard模块处理准静态非线性，Explicit模块处理中等速度冲击（如手机跌落），二者可无缝切换

阿喀琉斯之踵：

  • 上手门槛高：界面专业性强，学习曲线陡峭，缺乏”傻瓜式”教程[^29]
  • 计算效率：纯线性问题求解速度不如NASTRAN或ANSYS
  • 多物理场弱：流固耦合、电磁耦合能力不如COMSOL和ANSYS

适用场景： 汽车整车装配体分析、航空复合材料损伤、橡胶密封件设计、金属冲压成形、骨科植入物与骨骼接触分析。

4. MSC Marc —— 老牌非线性之”隐”

核心标签： 橡胶聚合物、网格自适应、学术积淀

Marc是专注于高度非线性分析的老牌软件，在橡胶、塑料领域有深厚积累。

独门绝技：

  • 材料 specialists：在超弹性体、粘弹性材料、高分子聚合物分析方面历史悠久
  • 网格重划分：大变形分析中可自动重划网格，避免单元畸变
  • 多物理场传统：早在90年代就具备热-机耦合能力

阿喀琉斯之踵：

  • 界面古老：被用户戏称为”DOS风格”，操作逻辑不符合现代软件习惯[^18]
  • 市场份额萎缩：新员工培训成本高，企业逐步转向ABAQUS

适用场景： 轮胎疲劳分析、高压密封圈老化、金属超塑性成形。

四、瞬态动力学阵营：毫秒间的”生死时速”

5. LS-DYNA —— 显式动力学之”神”

核心标签： 碰撞安全、爆炸冲击、侵蚀算法

当时间尺度进入毫秒级（如汽车碰撞），LS-DYNA是无可争议的霸主。其基于中心差分法的显式算法，无需迭代求解，直接推进时间步。

独门绝技：

  • 全自动接触：50+种接触算法，汽车碰撞中成百上千个零件的接触自动处理
  • 材料侵蚀（Erosion）：可模拟混凝土破碎、金属撕裂、玻璃飞溅等失效过程，这是隐式软件无法企及的能力[^25]
  • ALE/SPH算法：支持多物质流动（如油箱晃动、水体冲击），可处理大变形流体与固体交互

阿喀琉斯之踵：

  • 时间步长诅咒：显式算法需满足CFL条件，时间步长极小（微秒级），计算100ms物理时间可能需要数天
  • 准静态无力：不适合静态或低速问题，会发生”沙漏模式”等数值问题

适用场景： 整车碰撞安全（替代实车碰撞试验）、子弹穿甲、电子产品跌落、气囊展开、爆炸防护。

6. Altair HyperWorks（Radioss） —— 优化与碰撞之”侠”

核心标签： 拓扑优化、前处理、欧洲碰撞标准

HyperWorks是平台化工具，核心包含三部分：HyperMesh（前处理）、OptiStruct（优化/隐式求解）、Radioss（显式求解）。

独门绝技：

  • 前处理之王：HyperMesh的六面体网格划分技术、几何清理能力业界公认最强，支持输出给ABAQUS、ANSYS、LS-DYNA等所有主流求解器[^45]
  • 拓扑优化之父：OptiStruct首创商用拓扑优化，可从设计空间中自动生成”骨骼状”轻量化结构（如飞机肋板、发动机支架）[^43]
  • Radioss：欧洲汽车碰撞分析标准，与LS-DYNA并列为安全领域双雄，支持气囊折叠、假人定位等专业工具[^38]

阿喀琉斯之踵：

  • 求解器知名度：OptiStruct作为求解器在纯非线性分析市场占有率不如ABAQUS
  • 学习成本：网格划分技巧需长期积累，对新手不友好

适用场景： 白车身网格划分、航空航天结构轻量化设计、整车碰撞安全、创成式设计（Generative Design）。

五、专业领域阵营：细分场景的”专家号”

7. MSC NASTRAN —— 线性动力学之”尊”

核心标签： NASA血统、航空航天认证、NVH

诞生于阿波罗计划的NASTRAN，是航空航天结构分析的”贵族血统”。

独门绝技：

  • 认证标准：符合FAA/EASA适航要求，波音、空客结构强度报告的标准格式
  • 线性动力学权威：模态分析、频率响应、随机振动（PSD）、噪声（NVH）、气动弹性（颤振）算法积淀深厚
  • 求解效率：大型线性系统求解速度快，内存优化好[^26]

阿喀琉斯之踵：

  • 非线性短板：现代版本（SOL 400）虽加入非线性，但接触、大变形能力远弱于ABAQUS[^21]
  • 界面陈旧：前后处理常需配合Patran或FEMAP使用

适用场景： 飞机白机身模态、卫星结构动力学、发动机叶片振动认证、轨道交通NVH。

8. ADINA —— 流固耦合之”隐”

核心标签： FSI、土木工程、收敛稳定性

ADINA（Automatic Dynamic Incremental Nonlinear Analysis）专注于强耦合多物理场，尤其在流固耦合（FSI）领域独树一帜。

独门绝技：

  • 强FSI能力：采用直接耦合算法，处理血管与血液、大坝与洪水、油箱晃动等问题时稳定性极高，无需像ANSYS那样反复调试耦合参数[^36]
  • 非线性收敛：采用BFGS算法和自动时间步长，复杂接触问题几乎总能收敛[^29]
  • 源代码开放：提供部分Fortran源代码，便于科研修改

阿喀琉斯之踵：

  • 市场份额小：中国用户群体小众，教程和社区支持远少于ANSYS/ABAQUS
  • 前后处理弱：CAD接口和自动化能力落后于主流软件

适用场景： 心血管支架与血液流动、大坝抗震、储液罐地震响应、土木工程中的岩土非线性分析。

六、横向对比决策矩阵

软件最强项最弱项学习难度计算成本工业认证地位
COMSOL多物理场耦合（3+场）显式动力学/强接触非线性★★★☆☆高（多场耦合）★★☆☆☆
ANSYS工程多物理场流程复杂非线性收敛★★☆☆☆中等★★★★★
ABAQUS接触/材料非线性多物理场耦合繁琐★★★★☆高（非线性）★★★★☆
NASTRAN线性动力学/NVH非线性分析★★★☆☆低（线性）★★★★★（航空）
LS-DYNA碰撞/爆炸/侵蚀准静态问题★★★★☆极高（显式）★★★★★（汽车安全）
HyperWorks前处理/拓扑优化求解器知名度★★★★☆中等★★★☆☆
Marc橡胶/聚合物界面友好度★★★★★中等★★☆☆☆
ADINA流固耦合市场普及率★★★★☆中等★★☆☆☆

七、决策树：如何选择你的工具？

问题1：你的核心物理场是什么？

  • 结构为主 → 进入问题2
  • 结构+流体+电磁多场耦合 →
    • 若涉及微纳尺度或需自定义方程（如电池电化学反应）→ COMSOL
    • 若涉及宏观工程验证（如整车热管理）→ ANSYS
  • 纯流体/电磁 → 本文范围外（另见Fluent/CFX/HFSS专题）

问题2：结构分析的非线性强度？

  • 线性/小变形（弹性、小位移）→ NASTRAN（若航空）或 ANSYS（若通用）
  • 中度非线性（塑性、简单接触）→ ANSYS 或 ABAQUS
  • 高度非线性（大滑动接触、金属成形、复合材料失效）→ ABAQUS（首选）或 Marc（橡胶专用）

问题3：时间尺度与载荷类型？

  • 静态/准静态（秒级以上，如装配体压装）→ ABAQUS/Standard 或 ANSYS
  • 中速瞬态（毫秒级，如手机跌落）→ ABAQUS/Explicit
  • 高速冲击/爆炸（微秒级，如车祸、爆炸）→ LS-DYNA 或 Radioss

问题4：是否有优化需求？

  • 拓扑优化（轻量化设计）→ OptiStruct（HyperWorks）
  • 参数优化（尺寸优化）→ ANSYS 或集成HyperStudy

问题5：行业强制标准？

  • 航空结构强度认证 → NASTRAN（必需）
  • 汽车碰撞星级认证 → LS-DYNA 或 Radioss（必需）
  • 压力容器ASME认证 → ANSYS 或 ABAQUS

八、结语：工具链的”组合拳”

现代工程仿真已进入多工具协同时代，没有一款软件能通吃所有场景。理想的仿真部门工具链配置建议：

基础配置（覆盖80%场景）：

  • 前处理：HyperMesh（画高质量网格）
  • 通用结构：ABAQUS（非线性）+ NASTRAN（线性/航空）
  • 通用多物理场：COMSOL（早期概念设计）+ ANSYS（后期工程验证）
  • 安全分析：LS-DYNA（碰撞）

进阶配置（细分领域）：

  • 加入ADINA（水利/生物医学FSI）、Marc（橡胶件专项）等

黄金法则：

  • COMSOL 是探索未知的”显微镜”（微纳、多场、科研）
  • ABAQUS 是解构复杂结构的”手术刀”（非线性、接触）
  • LS-DYNA 是捕捉瞬间的”高速摄像机”（冲击、爆炸）
  • NASTRAN 是通向认证的”通行证”（航空线性规范）

理解每款软件的生态位，避免用COMSOL做整车碰撞（无显式算法），也别用LS-DYNA做微流控芯片（无微纳物理场），方能在仿真江湖中游刃有余。

参考资料： 本文技术细节综合自各软件官方文档、行业白皮书及资深CAE工程师实践经验。软件版本迭代迅速，具体功能请以最新发行版为准。