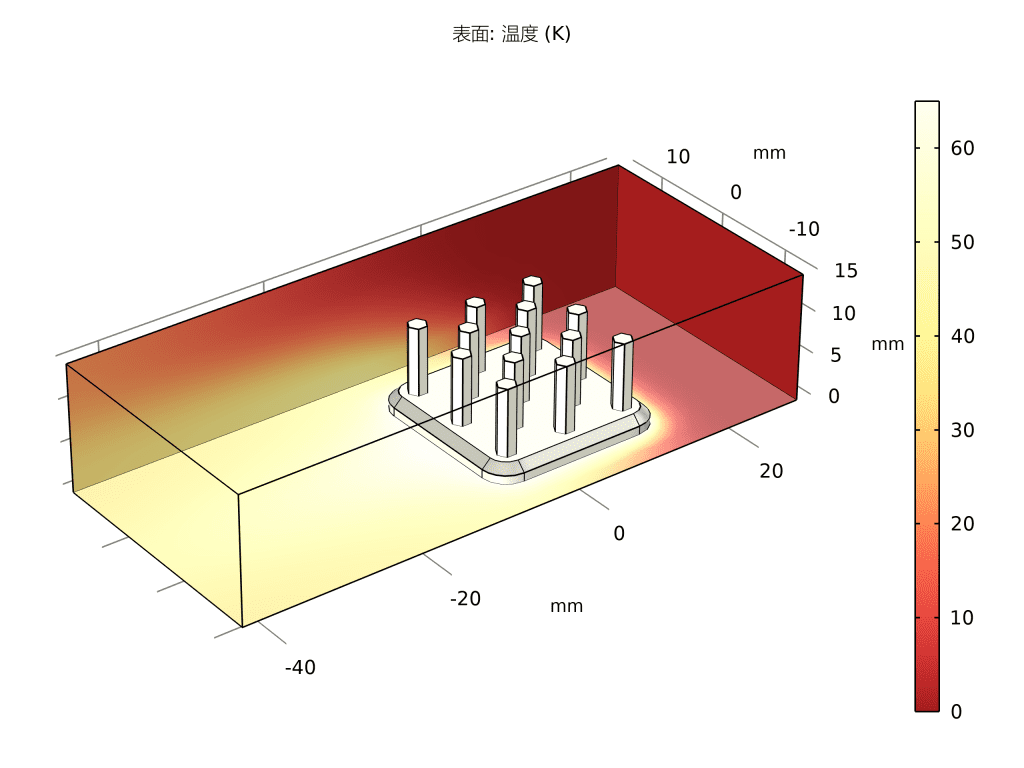
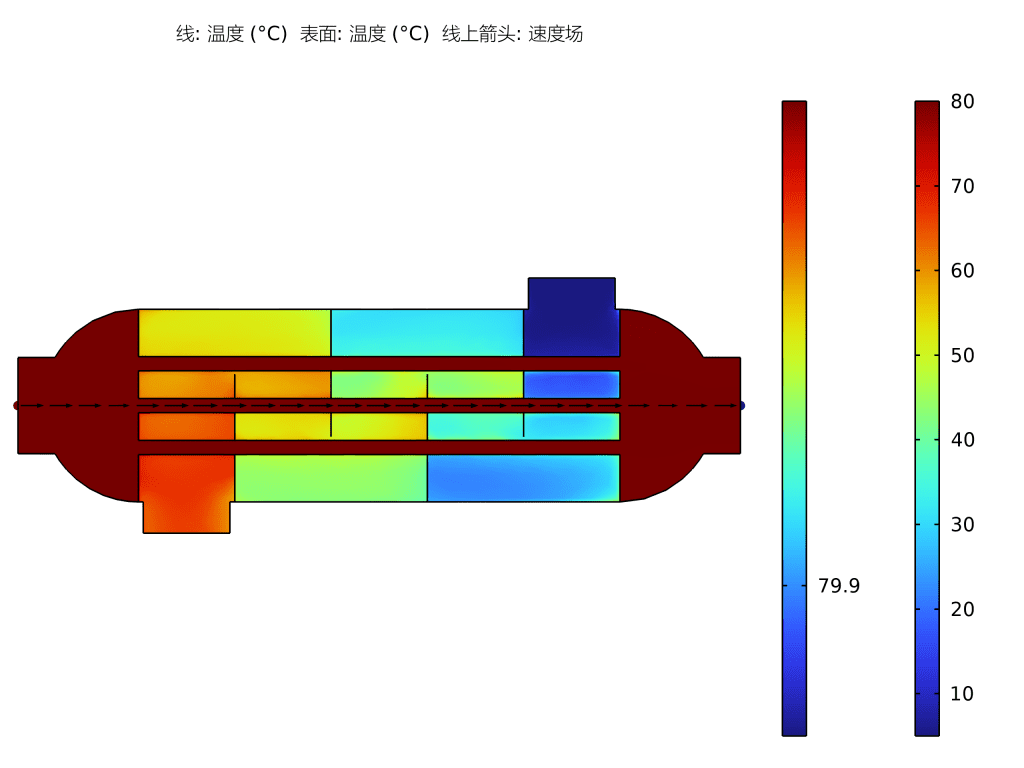
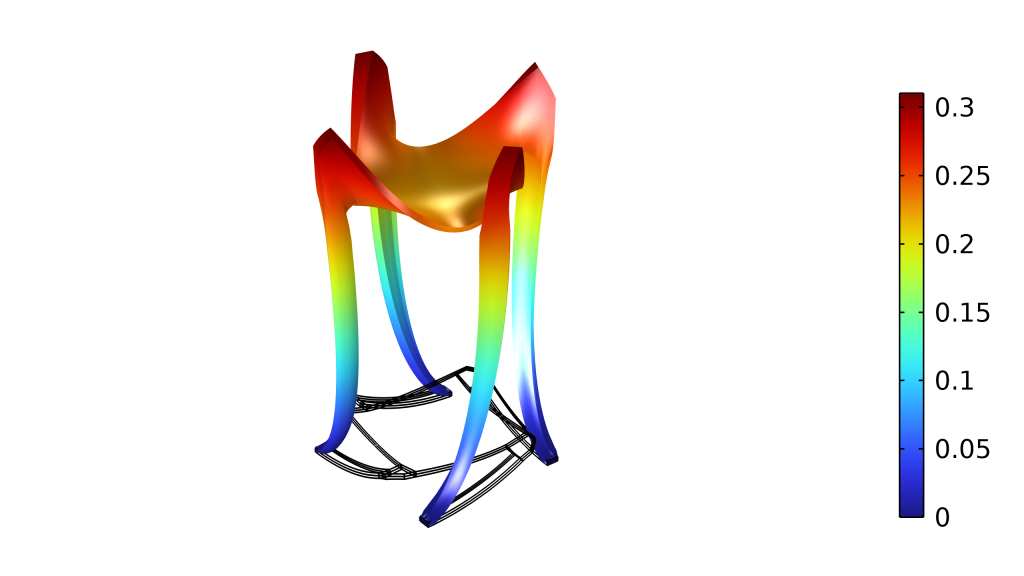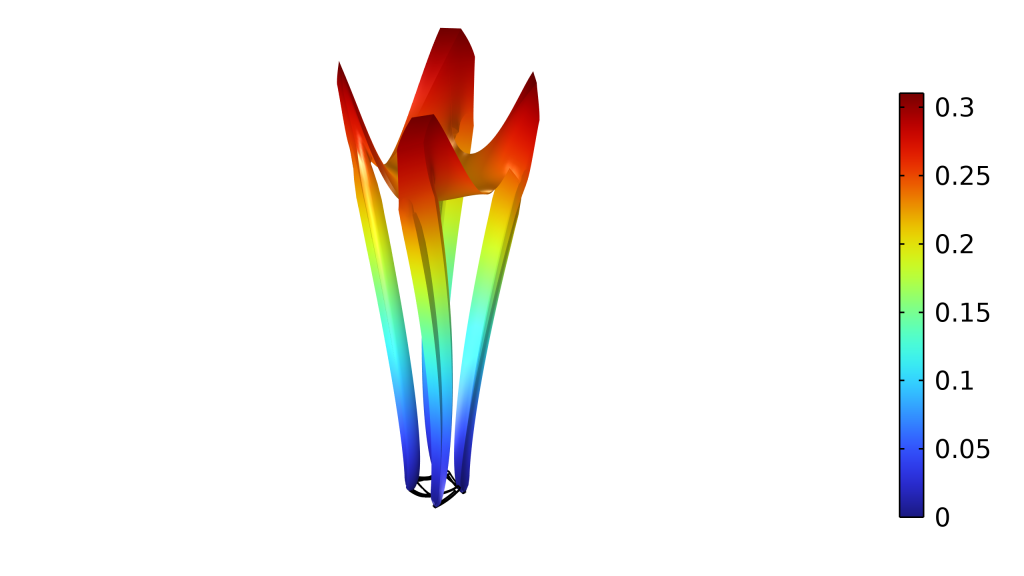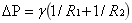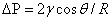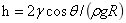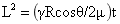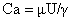毛细管力介绍
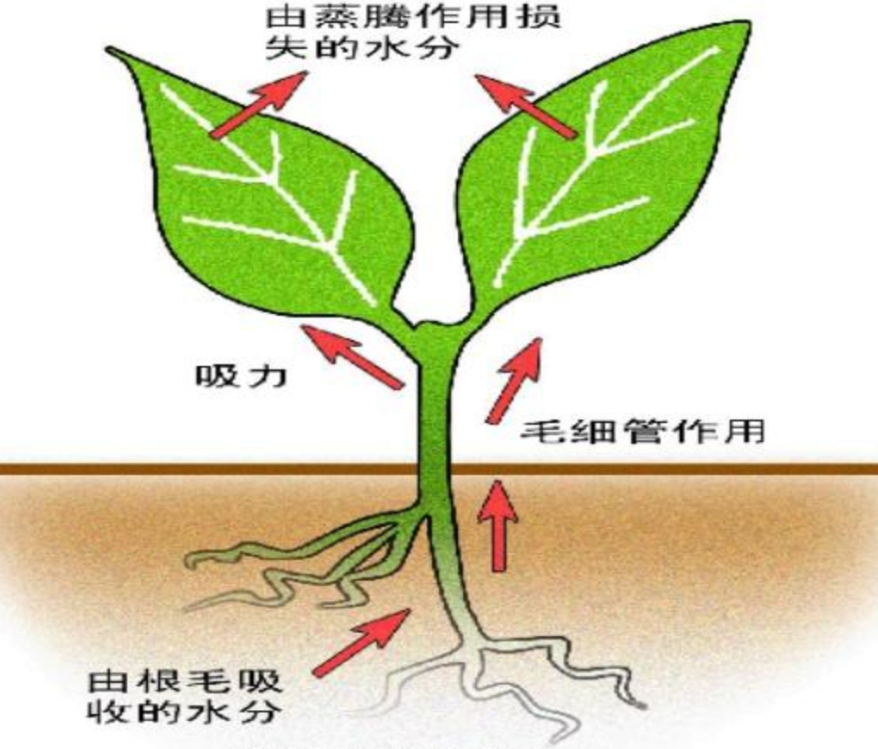
植物通过毛细作用将水分从根部输送到叶子,毛细管力使水能够沿着细管,即使在重力作用下也能持续输送;土壤中的孔隙可以看作是天然的毛细管,毛细管力帮助土壤保持水分,防止水分快速流失;在石油储层中,毛细管力是油水分离的关键因素。通过调节毛细管压力,可以优化石油的采收率;吸墨纸通过毛细作用吸收墨水,毛巾则利用毛细管力吸收水分,用于擦拭身体;油灯的灯芯通过毛细作用吸收油,使油能够持续燃烧,这些都是毛细现象,毛细现象不仅存在于我们的周围环境中,更在工业、农业、生物医学等领域发挥着至关重要的作用。



毛细管力是一种由液体表面张力引起的微观作用力,广泛存在于液体与固体界面或液体与液体界面之间。它源于液体分子之间的相互吸引力,这种吸引力使得液体表面倾向于最小化其表面积,从而产生表面张力。当液体进入细小的管道(毛细管)时,表面张力会驱动液体上升或下降,这种现象称为毛细作用。
毛细管力的大小与毛细管的半径、液体的表面张力、接触角以及液体的密度等因素密切相关。这种力在微观尺度上非常显著,甚至可以克服重力,使得液体在细小通道中自发移动。
要理解毛细管力,首先需要认识它的两个”基石”:表面张力和接触角。
表面张力和接触角
表面张力是液体表面分子间相互吸引的结果。液体内部的分子受到周围分子的均匀吸引力,而表面分子只受到下方和侧向的吸引力,这种不平衡导致液体表面趋向收缩,形成所谓的表面张力。表面张力的单位是N/m(牛顿每米),表示液体表面单位长度上的收缩力。
接触角则是描述液滴在固体表面上平衡时,液-气界面与固-液界面之间的夹角。接触角的大小由三种界面张力(固-气、固-液、液-气)的平衡决定,反映了液体对固体表面的”亲和力”:
接触角θ < 90°:液体润湿固体表面(亲水)
接触角θ > 90°:液体不润湿固体表面(疏水)
接触角θ ≈ 0°:完全润湿
接触角θ ≈ 180°:完全不润湿
液体的毛细行为强烈依赖于其润湿性:
亲液性系统(θ < 90°):液体在毛细管中上升,如玻璃管中的水;疏液性系统(θ > 90°):液体在毛细管中下降,如玻璃管中的汞。

润湿性不仅取决于液体性质,还与固体表面特性密切相关。通过表面处理(如等离子处理、化学涂层等)可以调控润湿性,从而控制毛细行为。
毛细管力最经典的数学表达来自杨-拉普拉斯方程,它描述了弯曲液面两侧的压力差(即毛细压力):

其中,ΔP是毛细压力(Pa),γ是液体表面张力(N/m),R₁和R₂是液面在两个正交方向上的曲率半径(m)。对于圆柱形毛细管中的液柱,曲率半径简化为R(毛细管半径),方程可简化为:

由此产生的毛细上升高度h可通过平衡毛细压力与静水压力得到:

其中,ρ是液体密度(kg/m³),g是重力加速度(m/s²)。
前述讨论主要关注平衡状态,而实际应用中往往涉及动态毛细过程。毛细渗透动力学:描述液体在多孔介质中前进的速度。经典的Washburn方程给出了圆柱形毛细管中液体前沿位置L与时间t的关系:

其中μ是液体粘度。该方程表明渗透距离与时间的平方根成正比。
毛细数(Ca):是粘性力与表面张力之比的无量纲数,用于表征动态过程中两种力的相对重要性:

Ca ≪ 1:表面张力主导(如毛细管中的液滴、微小尺度流动)。
Ca ≫ 1:黏性力主导(如高速流动或高黏流体中,表面张力影响可忽略)。
其中,U是特征速度。低毛细数时表面张力主导,高毛细数时粘性力主导。
仿真中的微流体
在COMSOL Multiphysics 中,模拟毛细管力相关现象时,通常会涉及以下几种物理场及其耦合:
1.两相流物理场
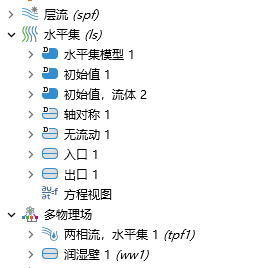
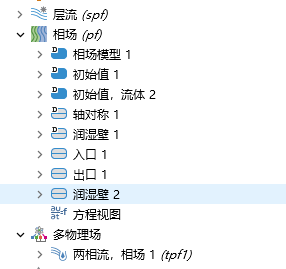
两相流物理场是模拟毛细管力现象的核心物理场之一,用于描述液体和气体之间的界面运动。COMSOL 提供了两种主要的两相流模型,水平集法和相场法。两相流,水平集方法通过水平集函数来追踪流体界面,适用于界面清晰且需要精确捕捉界面位置的情况。两相流,相场方法则是使用相场变量来描述流体界面,适用于界面较为模糊或需要考虑界面扩散的情况。根据comsol官网案例,可对比毛细管填充案例,水平集法和相场法边界条件设置的差异性。
水平集法:

相场法:


2、多孔介质物理场
当模拟多孔介质中的毛细现象时,会用到以下物理场:
多孔介质相传递:用于模拟多孔介质中不同相(如液体和气体)的输运过程,考虑了相对渗透率和毛细压力。
达西定律:描述流体在多孔介质中的流动,常与多孔介质相传递物理场耦合,用于计算流体的流动速度。
根据comsol官网案例,可了解低渗透性晶体上方的两相流 案例的边界条件设置


3、其他相关物理场
静电场:在某些情况下,如电场驱动的毛细现象(如泰勒锥),需要耦合静电场物理场来模拟电场对流体界面的影响。
润湿壁边界条件:用于设置流体与固体壁面之间的接触角,这对于模拟毛细管力的驱动和阻力至关重要。
微流体设计在前沿应用
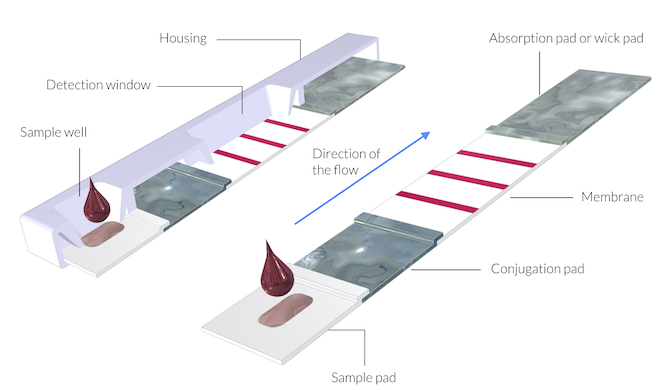
纸基微流体(Paper-based Microfluidics):用于低成本即时诊断(如COVID-19检测试纸),依赖毛细作用实现样本自动分配。侧向流免疫层析测定法(LFIA)或免疫层析试验用来快速检测新冠。

单细胞分析:毛细微阱(Microtraps)捕获单个细胞,结合荧光检测研究细胞异质性。
汗液传感:基于毛细作用的微通道收集汗液,实时监测葡萄糖、乳酸(如加州理工的“皮肤贴片传感器”)。
微尺度相变传热:毛细力驱动冷却液在微热管(Heat Pipe)中循环,用于电子器件散热。
毛细驱动微型机器人:通过表面张力梯度操控液滴移动(如磁性液滴机器人用于靶向给药)。
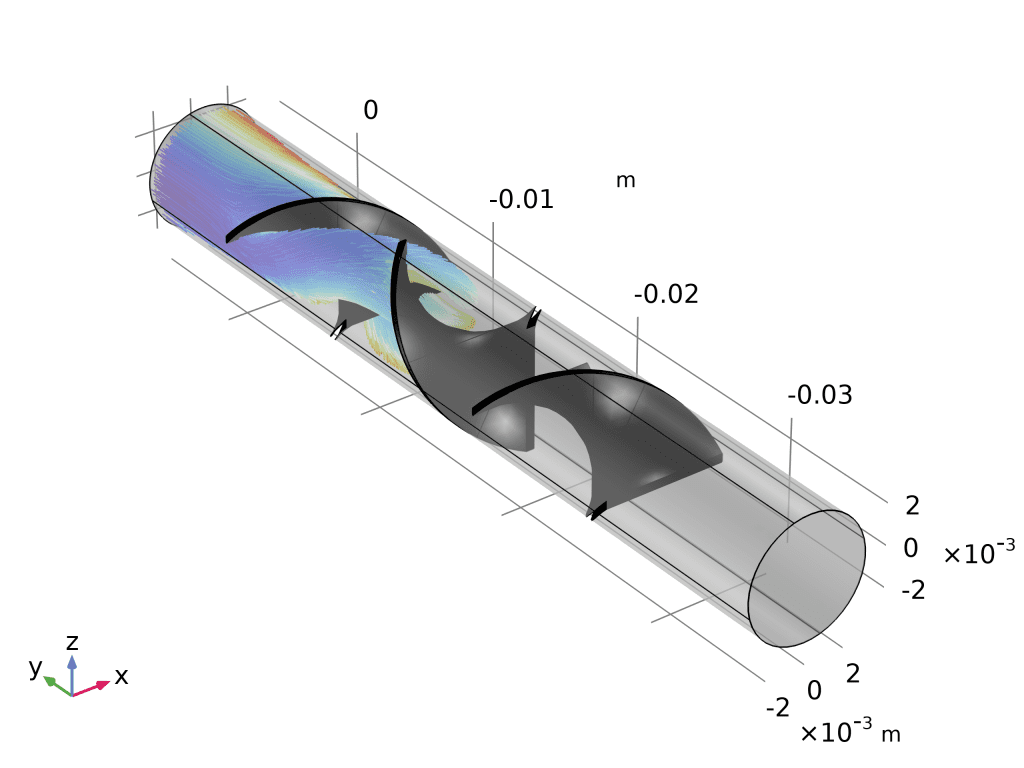
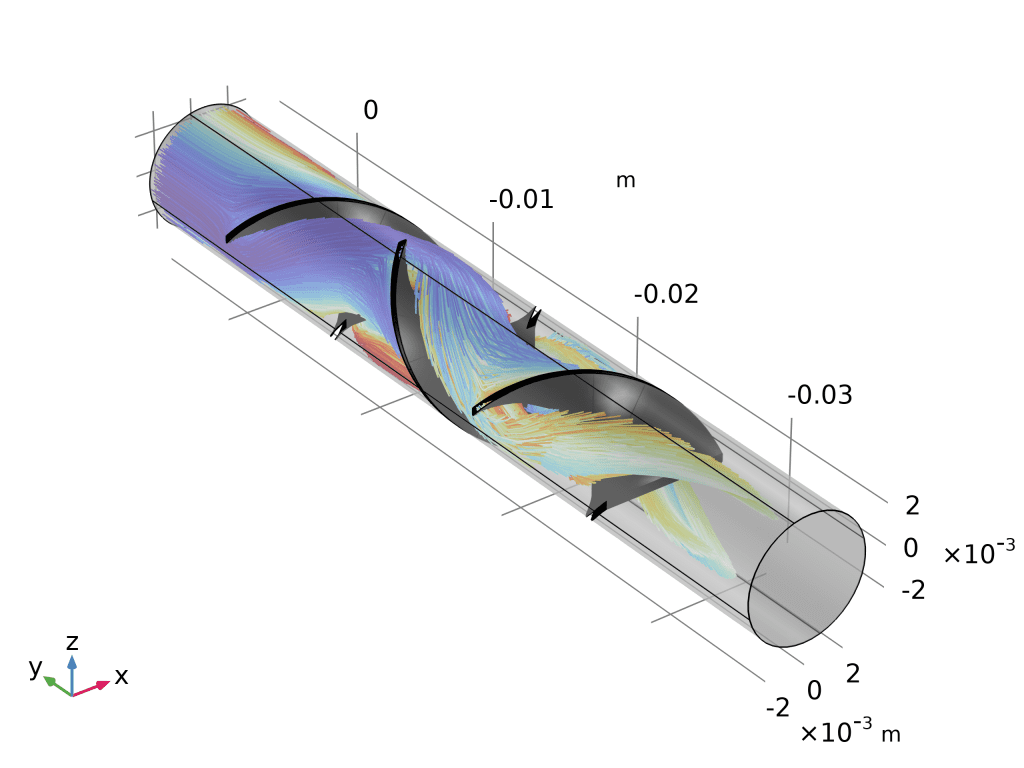
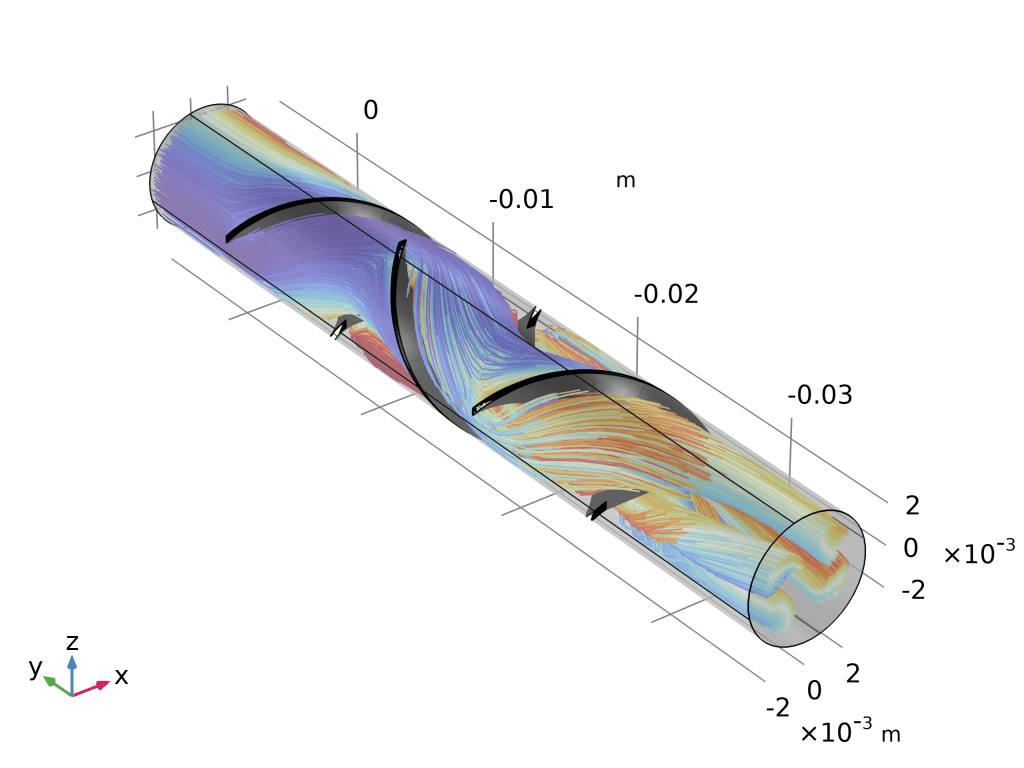
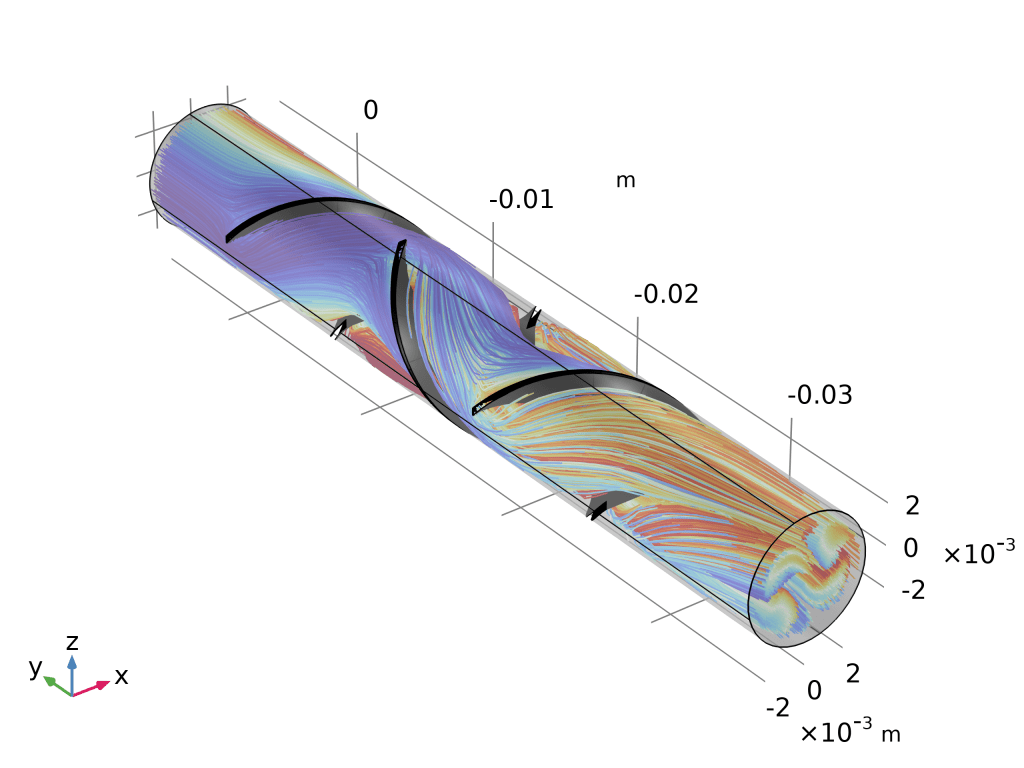
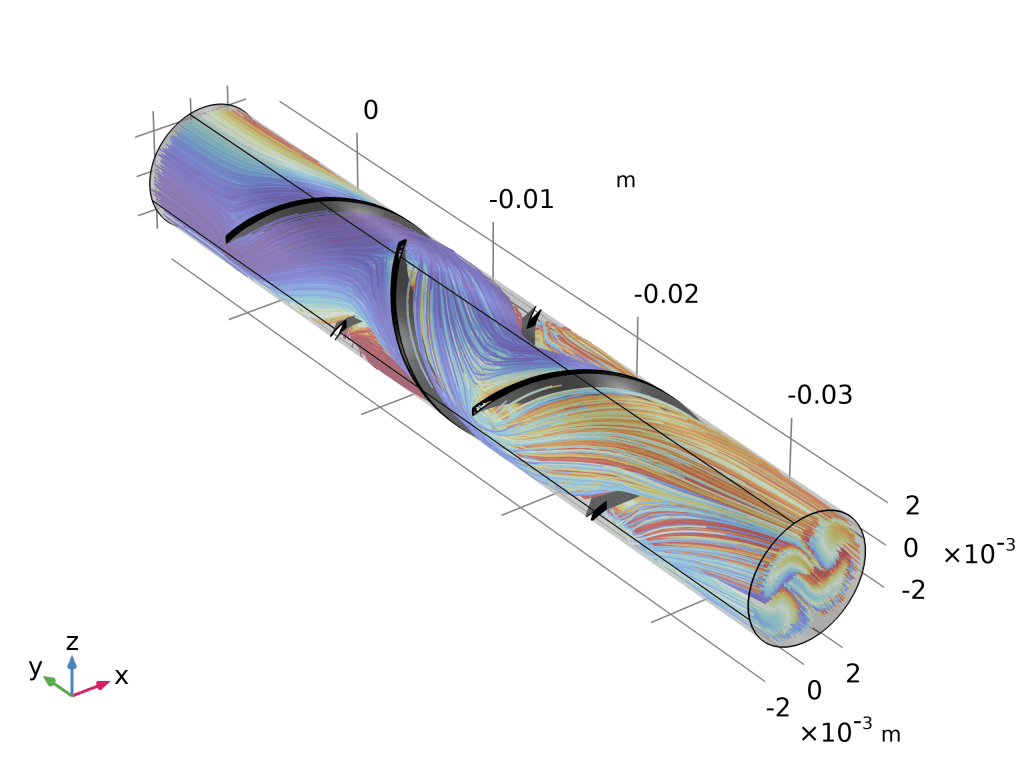
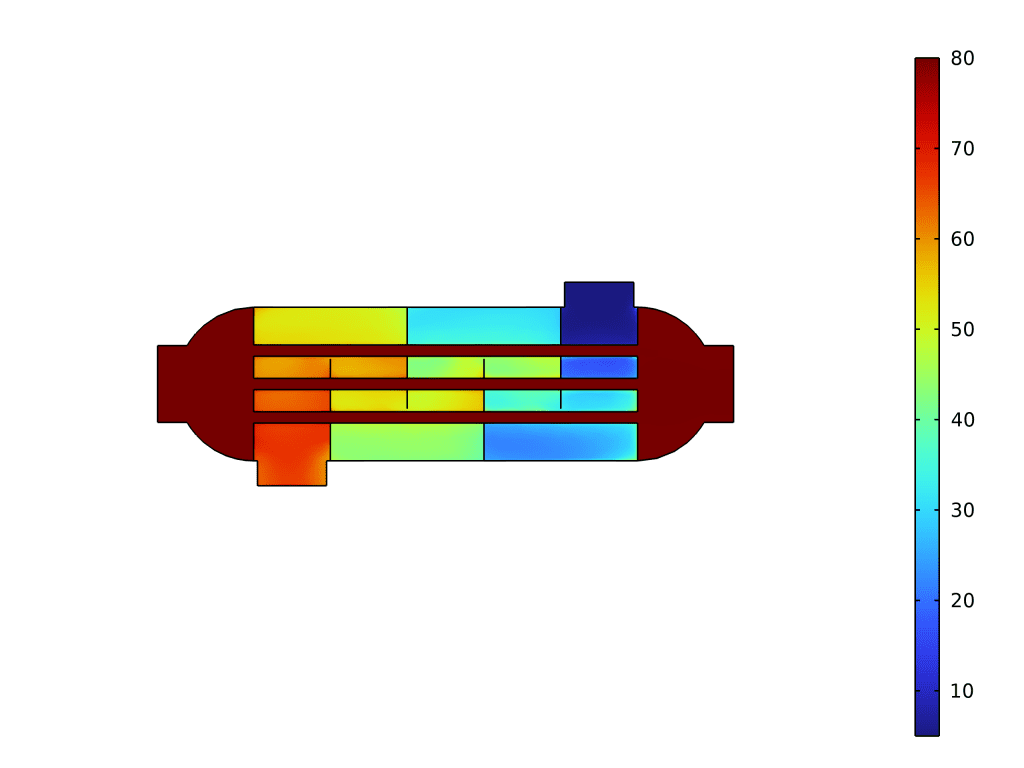
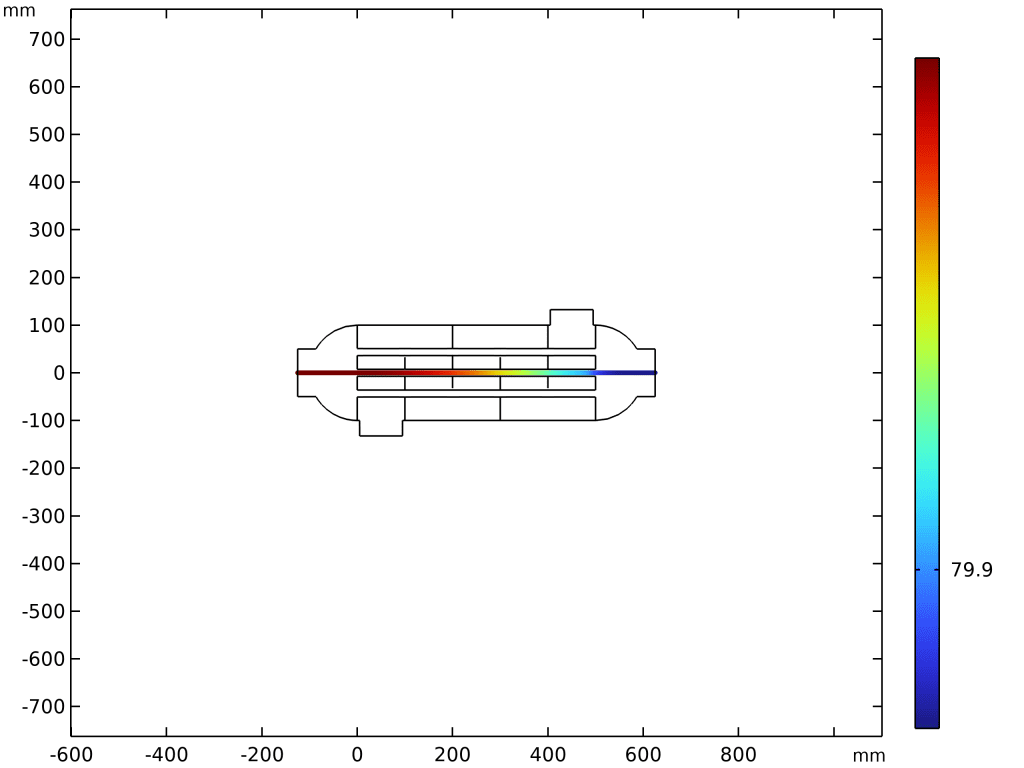
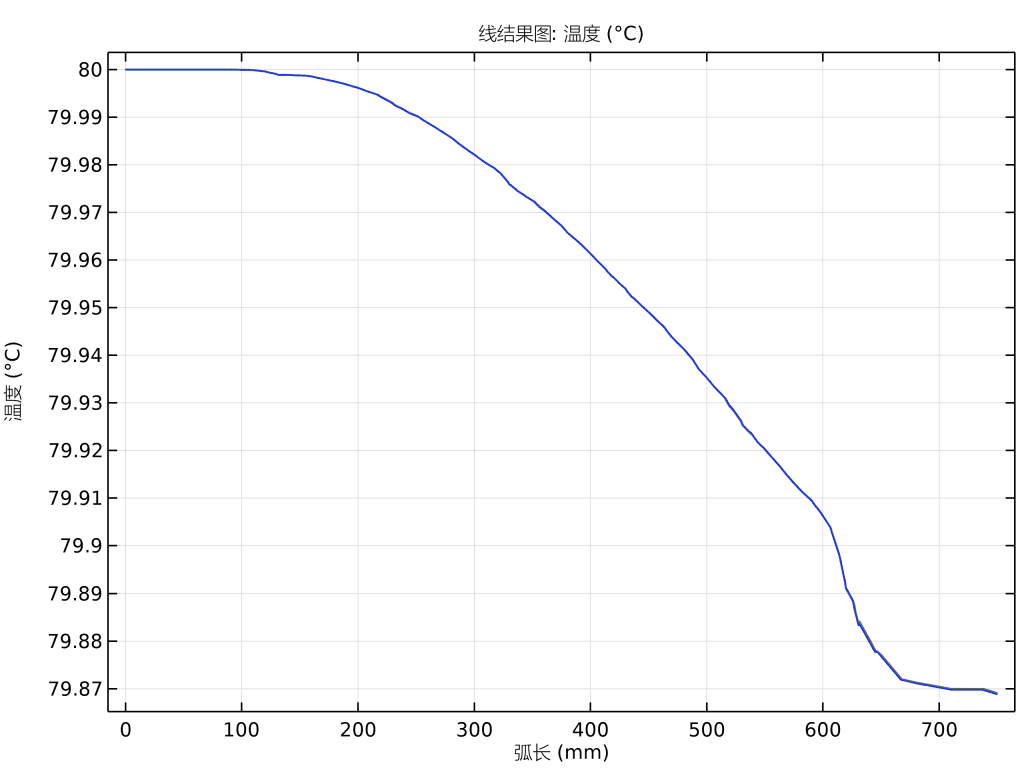
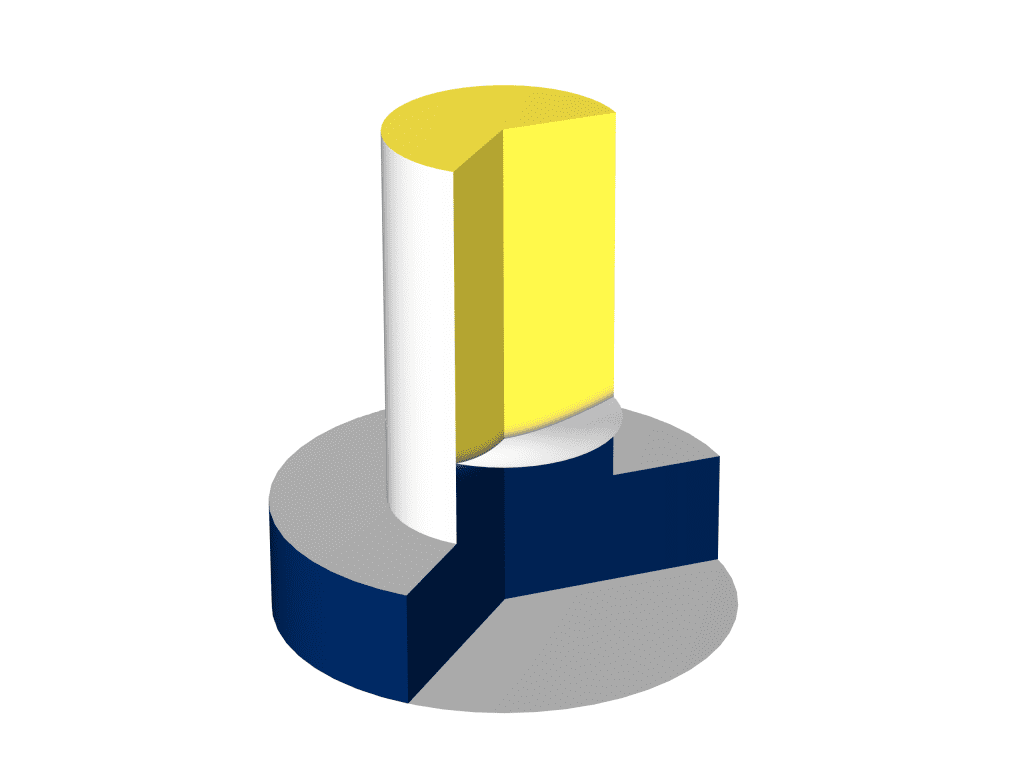
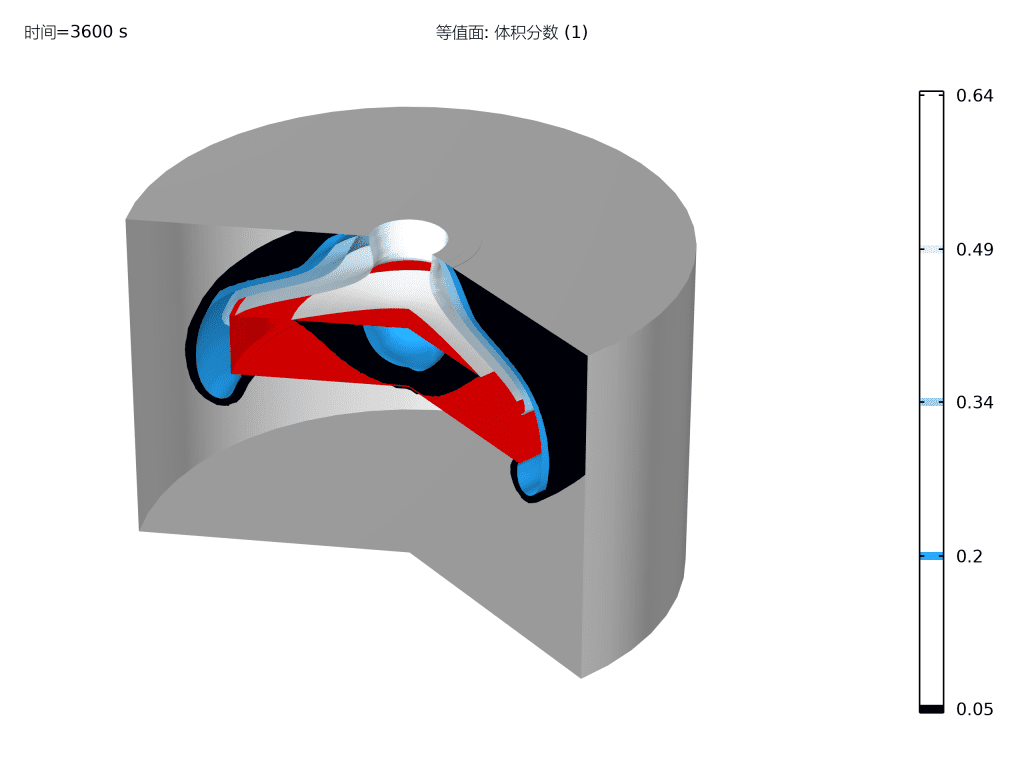
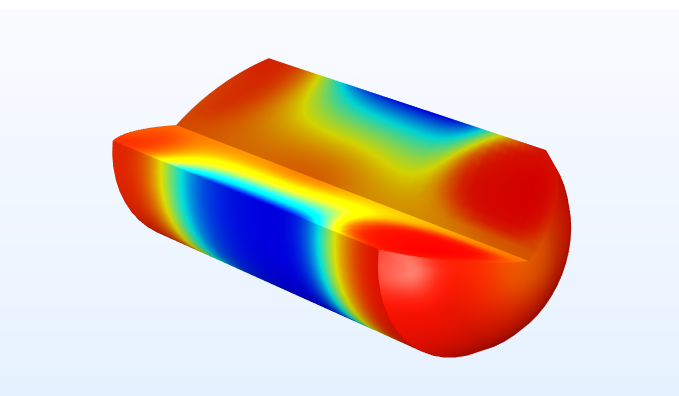
药物输送系统:此处显示的模型描述了提供可变浓度的水溶性药物的药物输送系统的操作。在仿真中,固定体积和速度的液滴沿毛细管向下流动。毛细管壁的一部分由渗透膜组成,该渗透膜将毛细管内部与药物的浓溶液分开,该浓溶液在通过时会溶解到水滴中。通过改变液滴速度,可以调节液滴中药物的最终浓度。

液滴微流场技术:液滴微流场 技术能够形成大量均匀、可控和独立的小液滴。该场对于持续生成多乳液滴特别有用。多核乳液滴可用于生成具有特定排列的类似细胞内部结构的微尺度颗粒,从而在不同的生物工程学科中实现程序化的化学相互作用。(http://cn.comsol.com/blogs/analyzing-a-new-droplet-forming-fluidic-junction-with-simulation)



毛细管力虽然源自微观尺度的分子相互作用,却在宏观世界展现出广泛而深远的影响。随着纳米技术、生物技术等领域的快速发展,对毛细现象的理解和控制将变得更加重要。掌握这一”微观”力量,或许将帮助我们解决许多”宏观”难题,为可持续发展提供新的解决方案。
毛细管力相关comsol案例可参考学习:
毛细管填充:相场法、水平集法相关案例
http://cn.comsol.com/model/capillary-filling-1878
低渗透性晶体上方的两相流:多孔介质相传递、达西定律
http://cn.comsol.com/model/two-phase-flow-over-a-low-permeable-lens-68081