吃透 COMSOL 后处理（四）：专业图表与特殊应用——满足你的“小众”需求

开篇引言：

“基础操作已经熟练，数据也能剖析得明明白白，但客户或审稿人总嫌‘不够专业’？远场辐射图、粒子轨迹、相图、庞加莱图……这些听起来‘高大上’的专用图表，其实只需几步就能在 COMSOL 里一键生成。今天，我们走进‘专业频道’，让报告瞬间拥有学术会议海报的既视感。”

正文核心：

1. 远场图（Far-Field Plot）：把天线辐射搬上‘球幕影院’

痛点：RF、天线、声学设备最关注“远区”辐射特性，却苦于无法在三维云图里一眼看出方向性。
解决方案：使用“远场图”，把计算得到的远场变量映射到虚拟球面，球面半径=场强，自动随角度变形。
实操案例：
1. 打开 “基片集成波导（SIW）漏波天线”（RF 模块 > Antennas）。
2. 结果 → 三维绘图组 → 远场图 → 选择“Far-Field Domain”数据集。
3. 表达式填入 emw.normEfar，θ/φ 分辨率拉到 180（最高平滑度）。
4. 一键“球幕”：图形窗口瞬间出现一张“变形地球仪”——高场强方向球面鼓出，低场强凹陷；主瓣、旁瓣、后瓣尽收眼底。
5. 学术级操作：把 θ 裁剪到 0–90°，φ 固定 0°，再叠加 2D 极坐标远场切面，一张图同时给出 3D 立体与 2D 切面，论文插图直接达标。

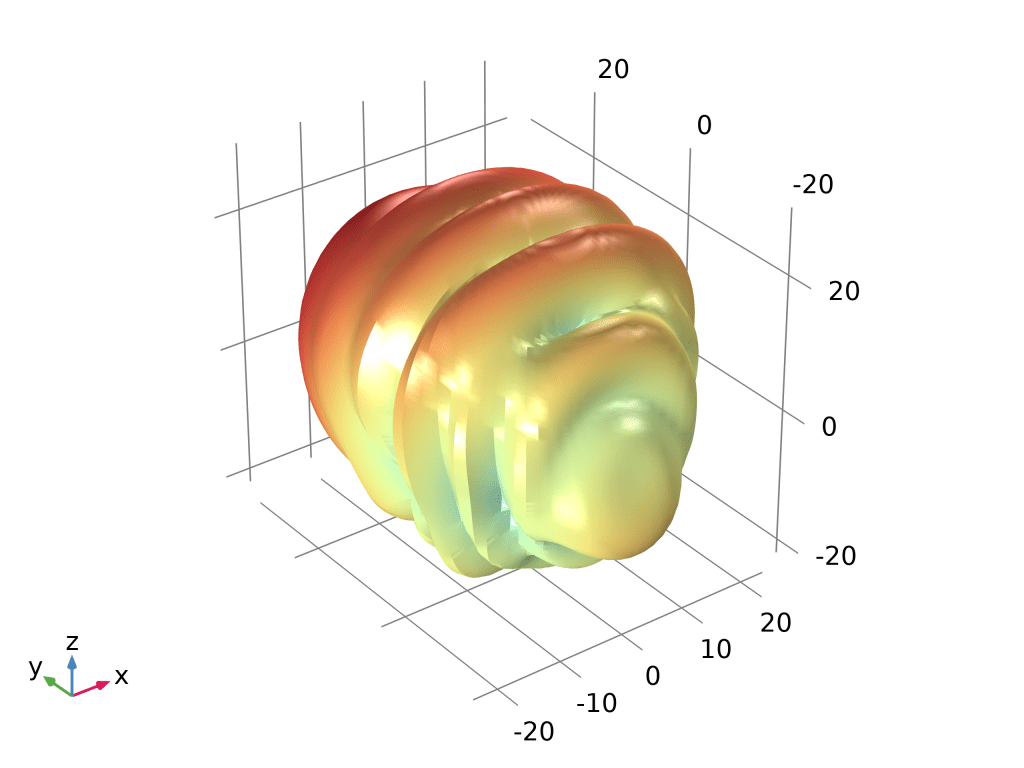
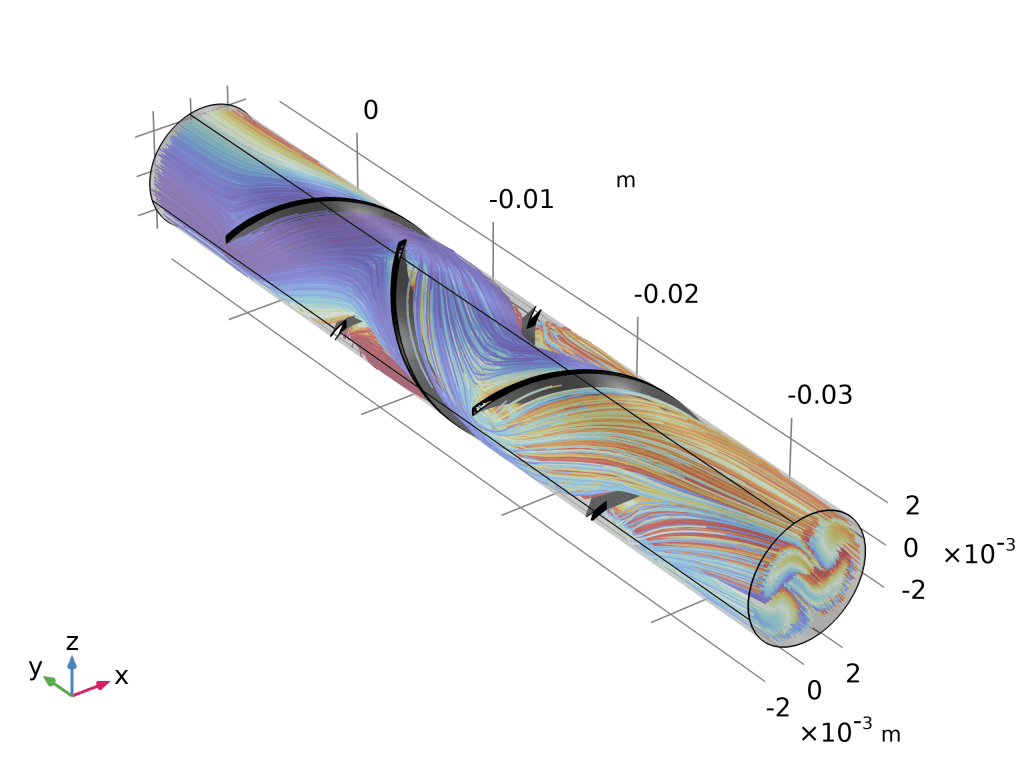
2. 粒子追踪图：让‘离散’粒子替你说清混合效率

痛点：微流道、质谱仪、行星轨迹等场景，连续流线无法反映“单个粒子”惯性、扩散或交界面统计。
解决方案：调用“粒子追踪”专用绘图，把每一粒子的常微分方程解可视化，再搭配“相图”“庞加莱图”做统计。

实操案例：

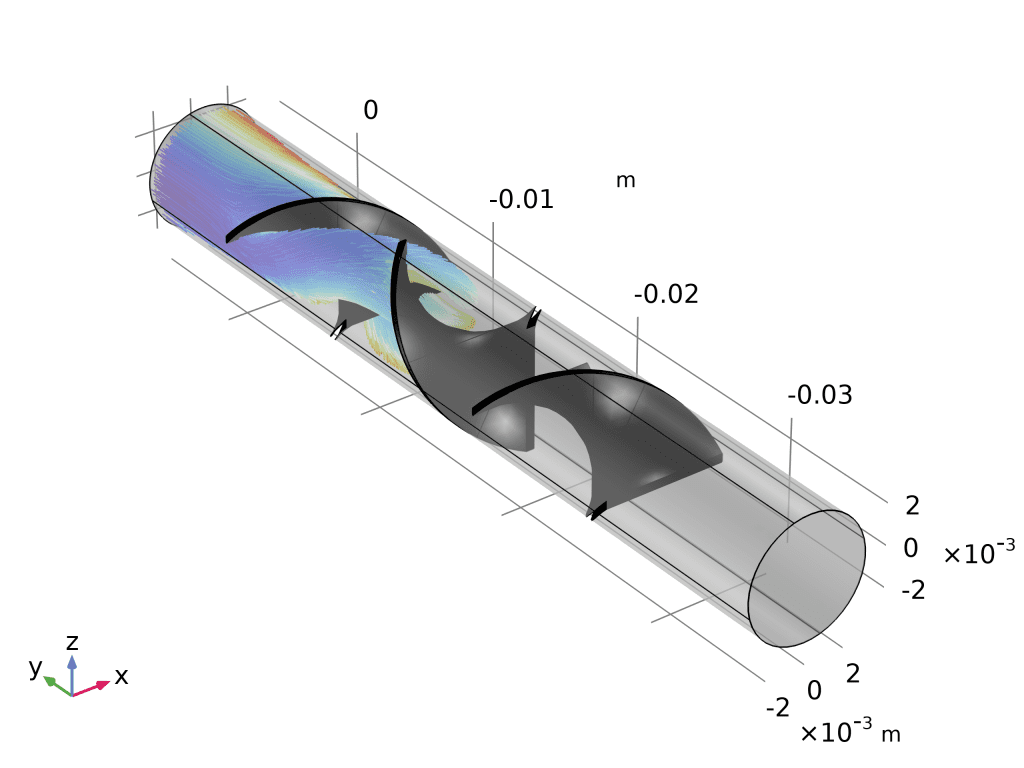
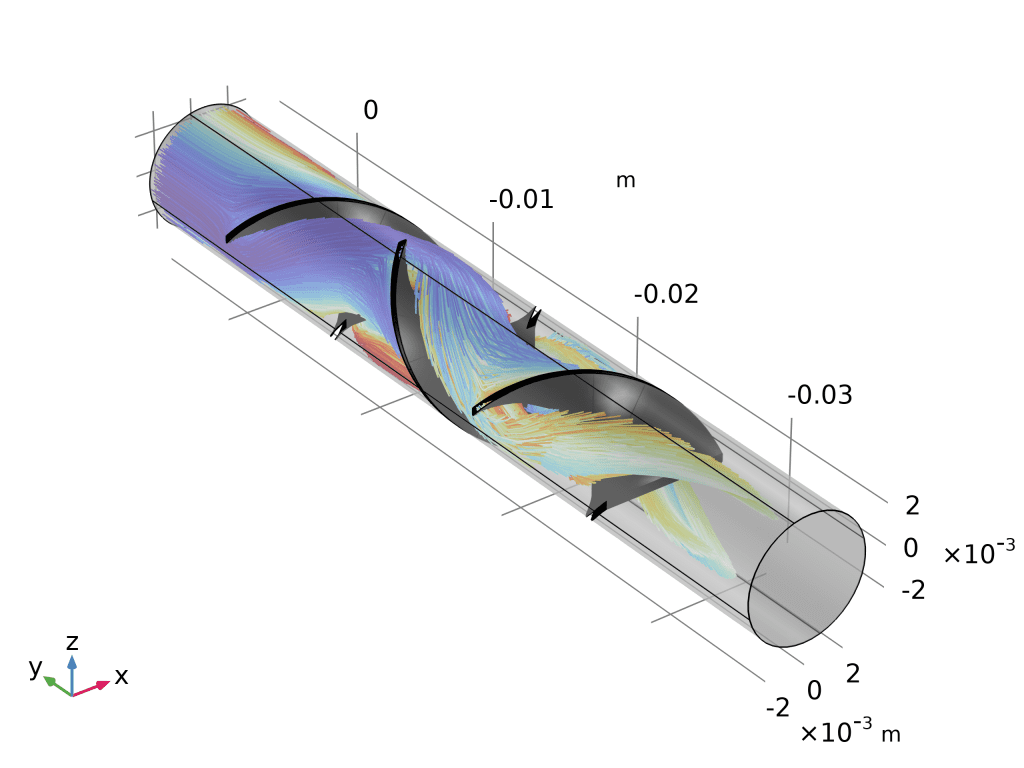
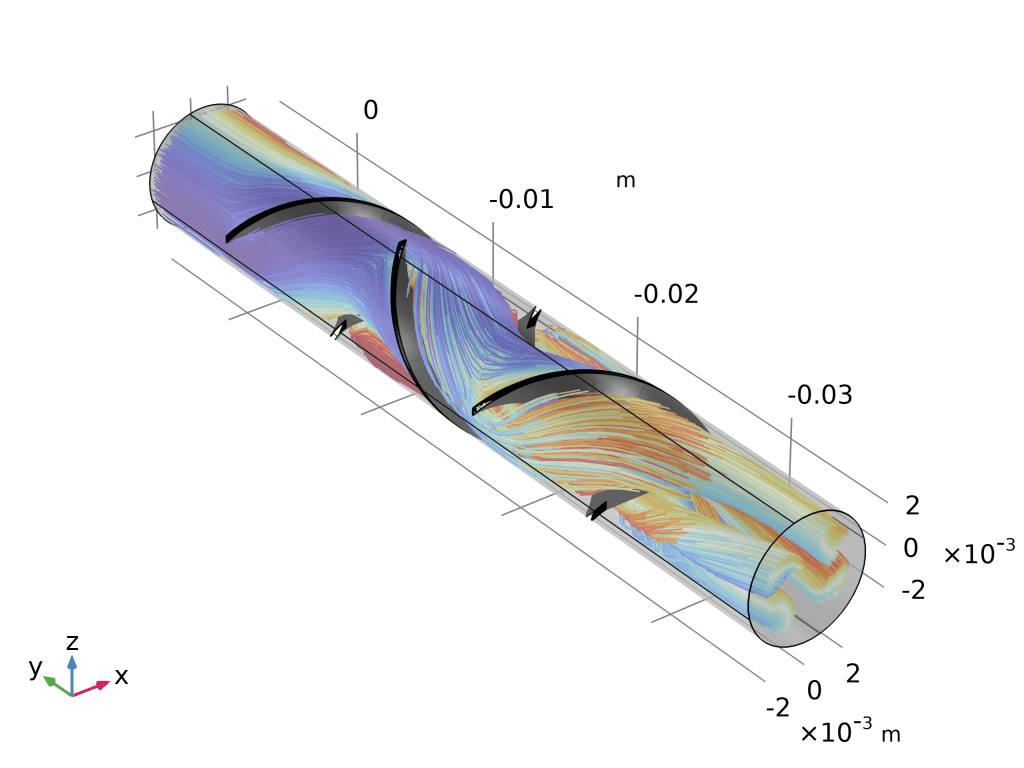
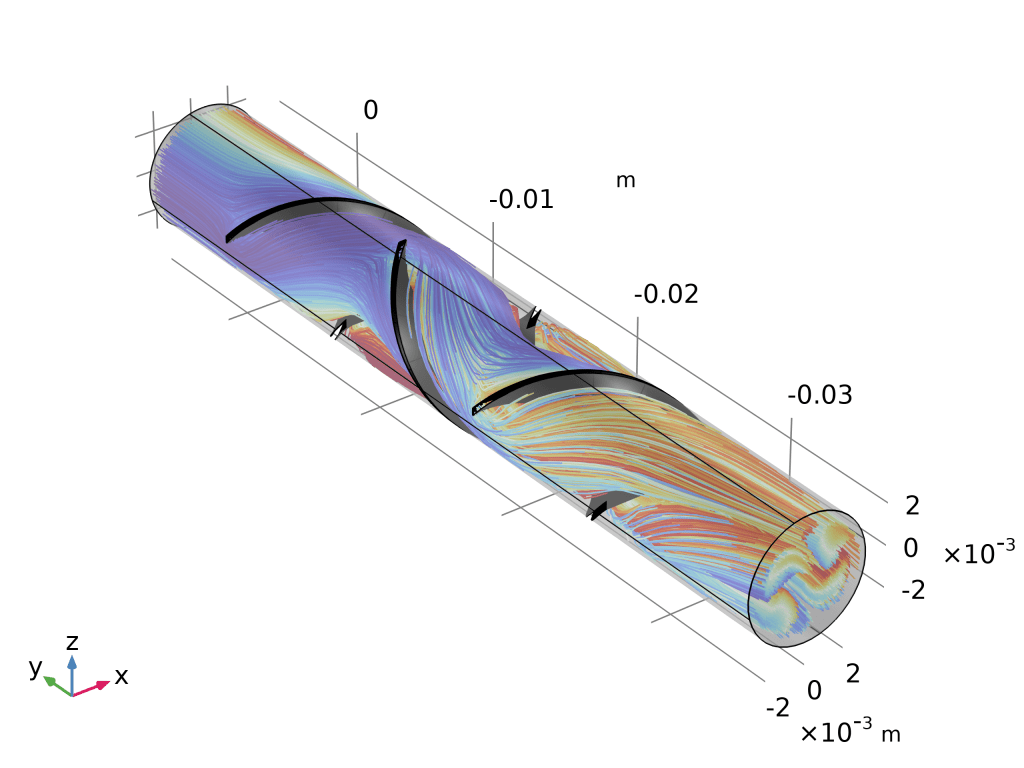
打开 “静态混合器粒子追踪”（粒子追踪模块 > Fluid Flow）。
轨迹图：
- 三维绘图组 → 粒子轨迹 → 数据集选“Particle Trajectories”。
- 颜色表达式改为 spf.U，瞬间看到粒子从入口到出口的速度演化。

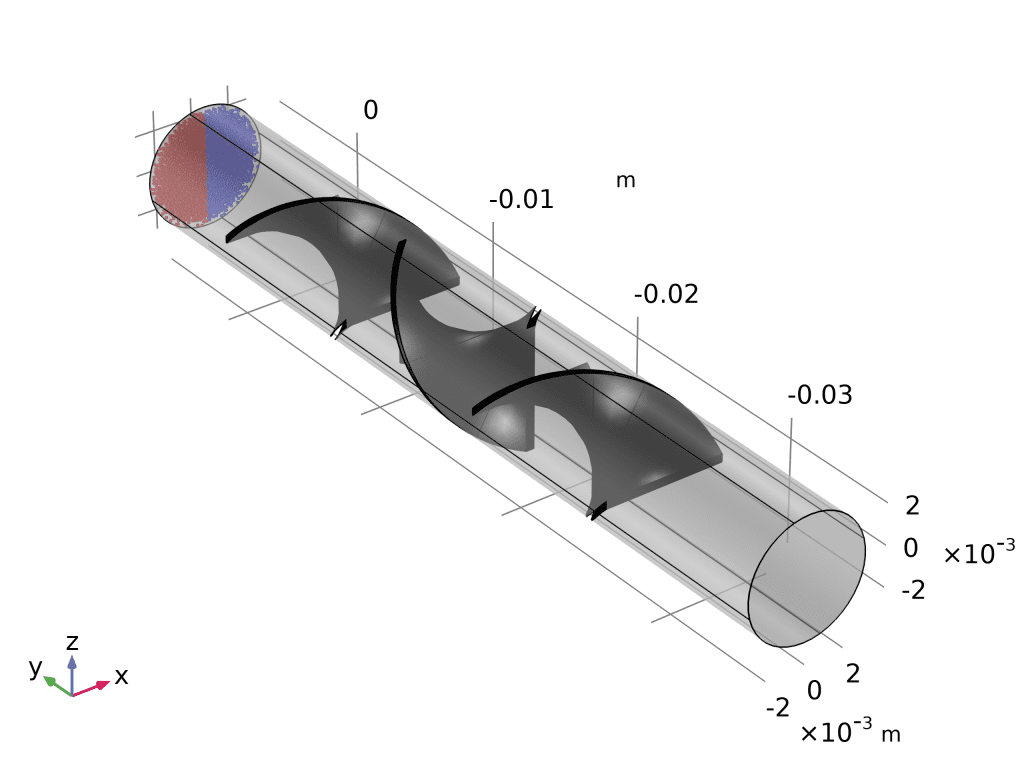
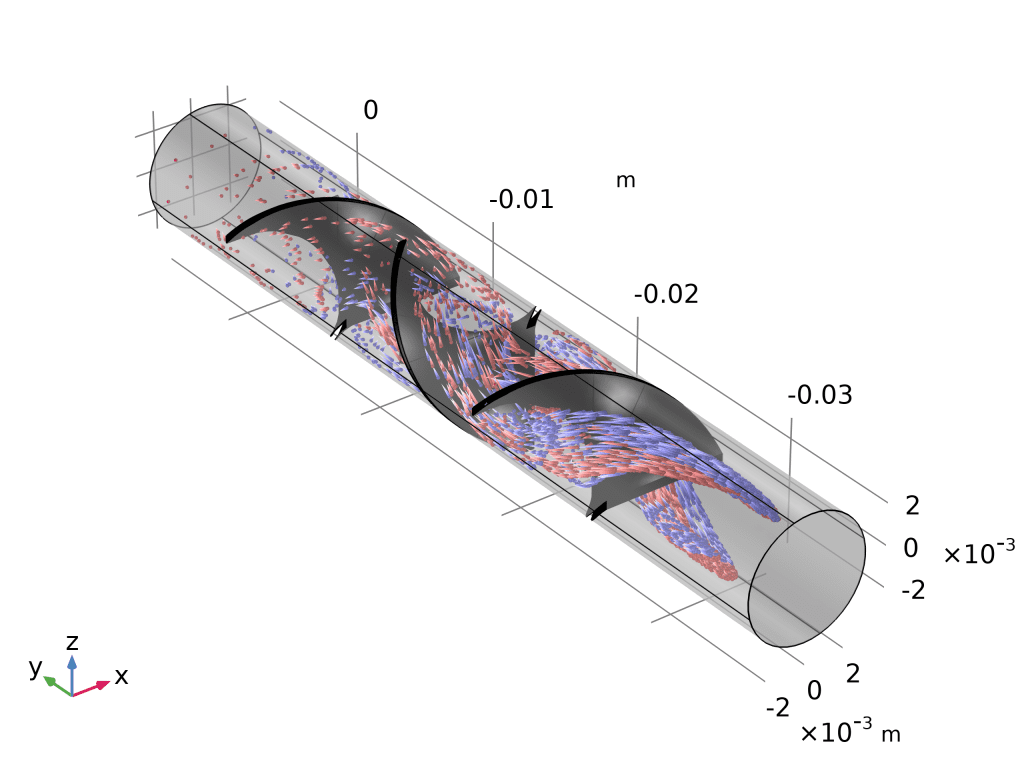
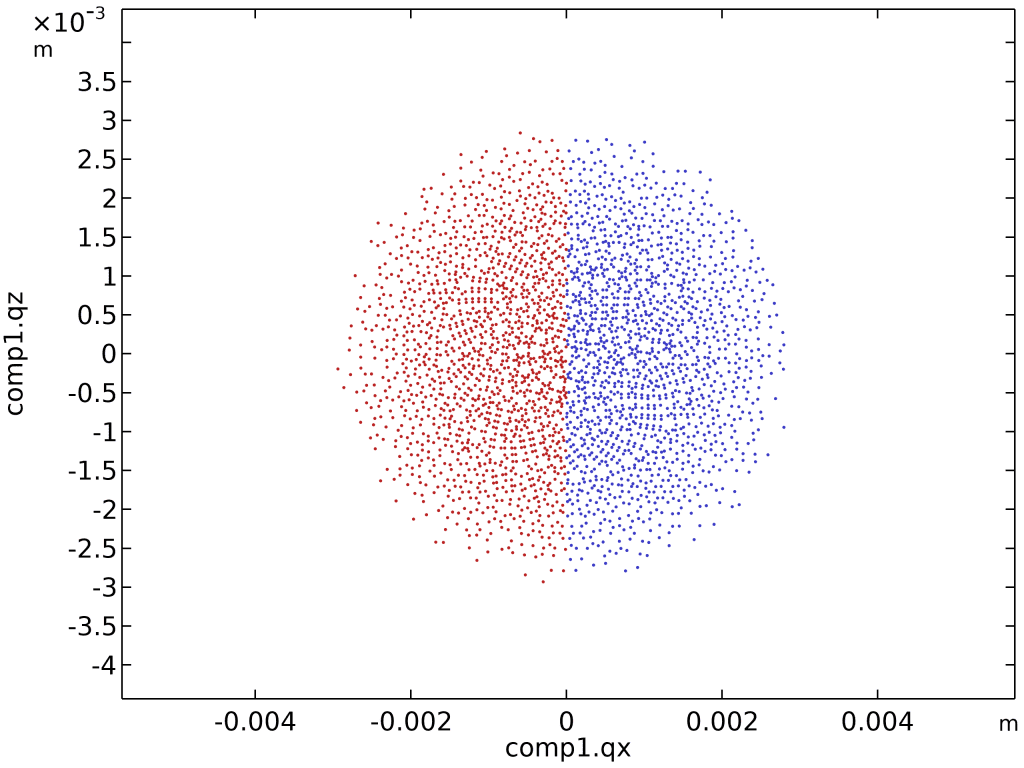
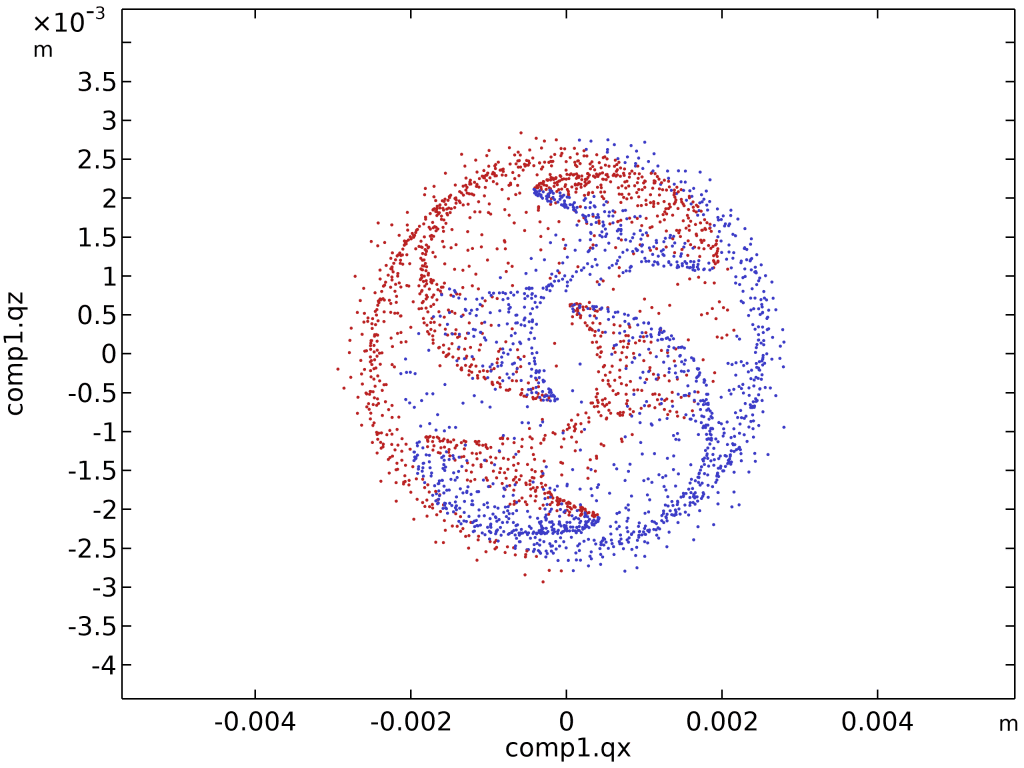
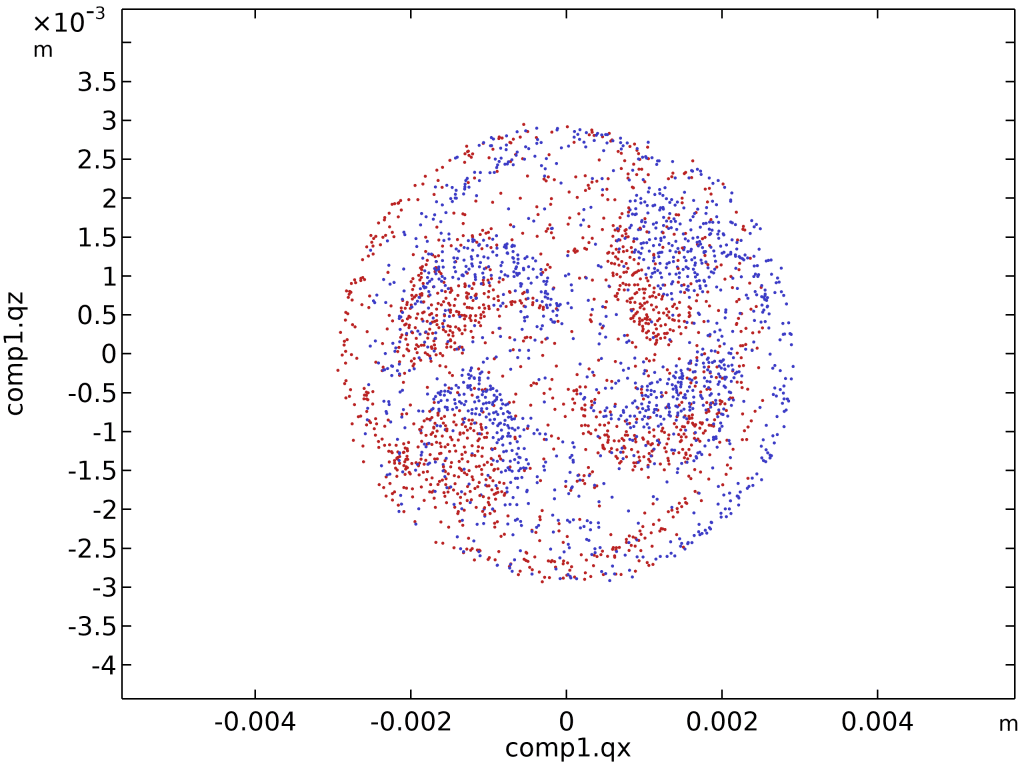
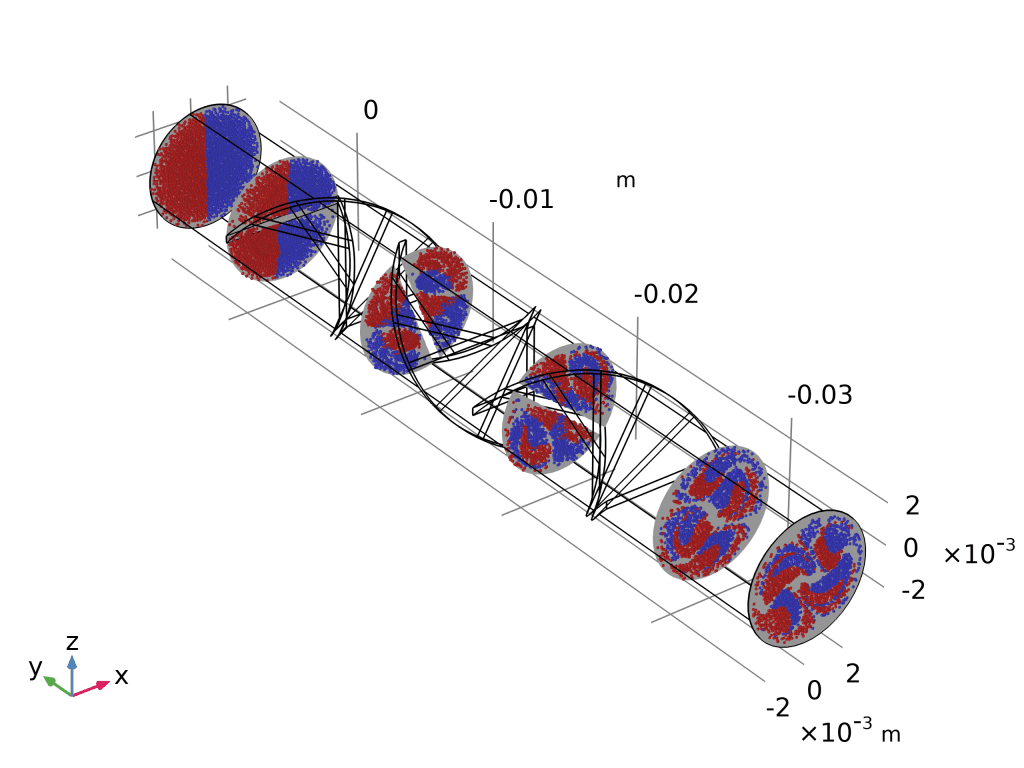
相图（Phase Portrait）：
- 二维绘图组 → 相图 → 坐标轴选 x 与 y 横向位置。
- 时间选 t = 4.2 s，颜色按初始 y 坐标着色。
- 结果：红蓝两团粒子依旧泾渭分明，混合效率一目了然。

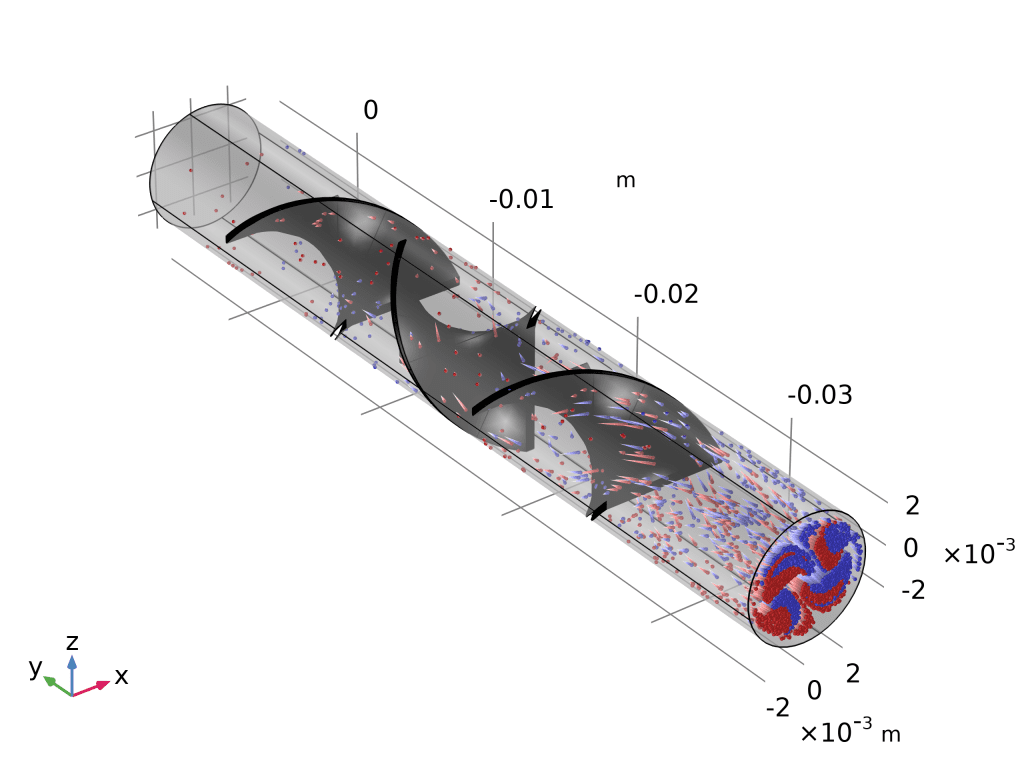
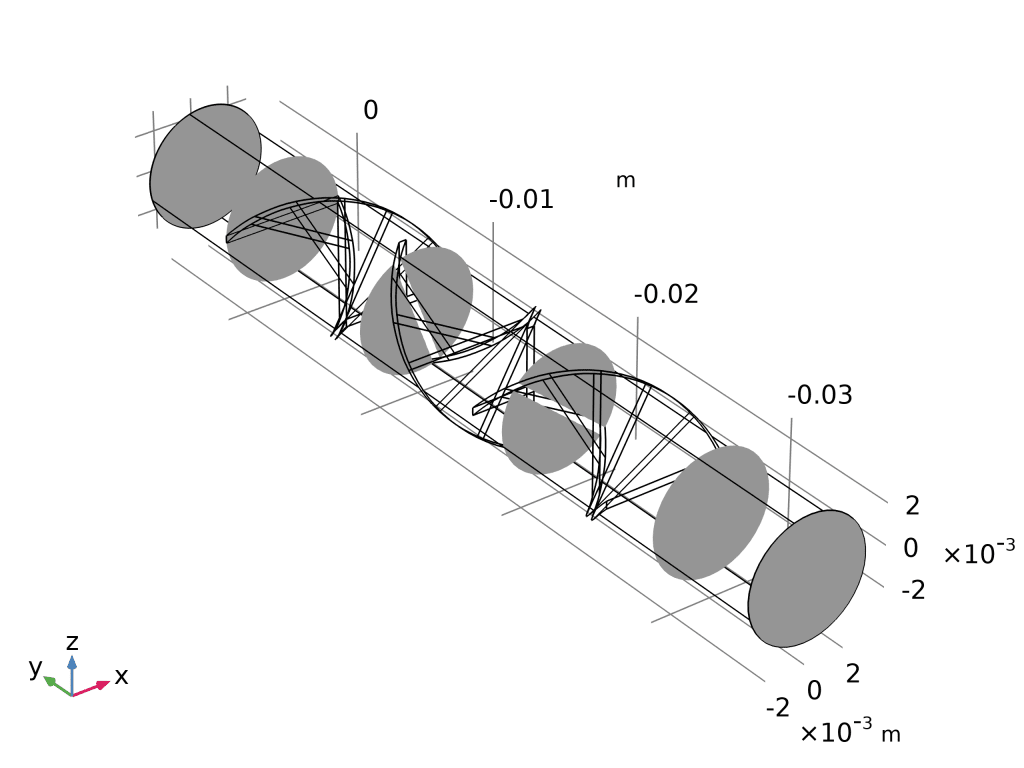
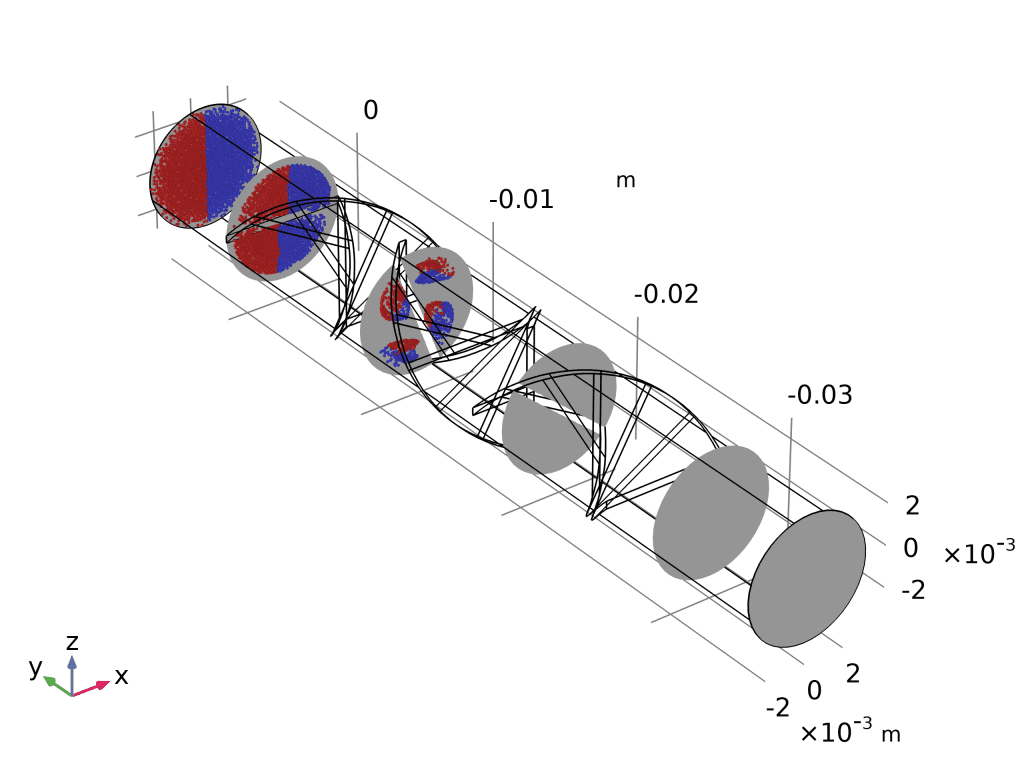
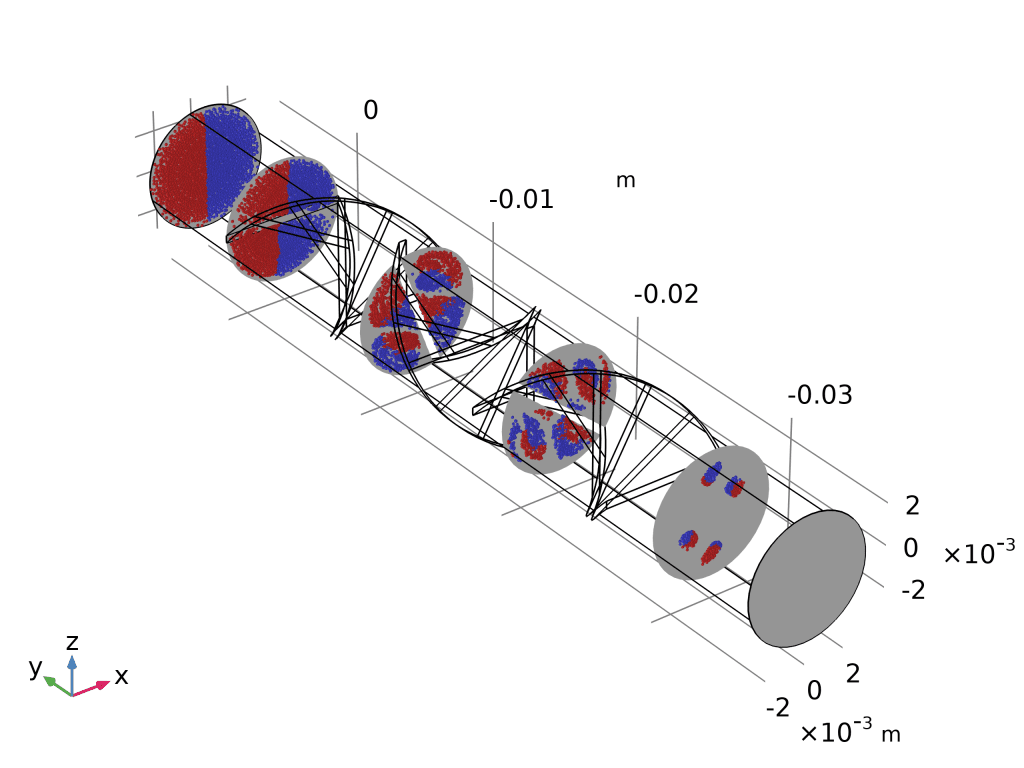
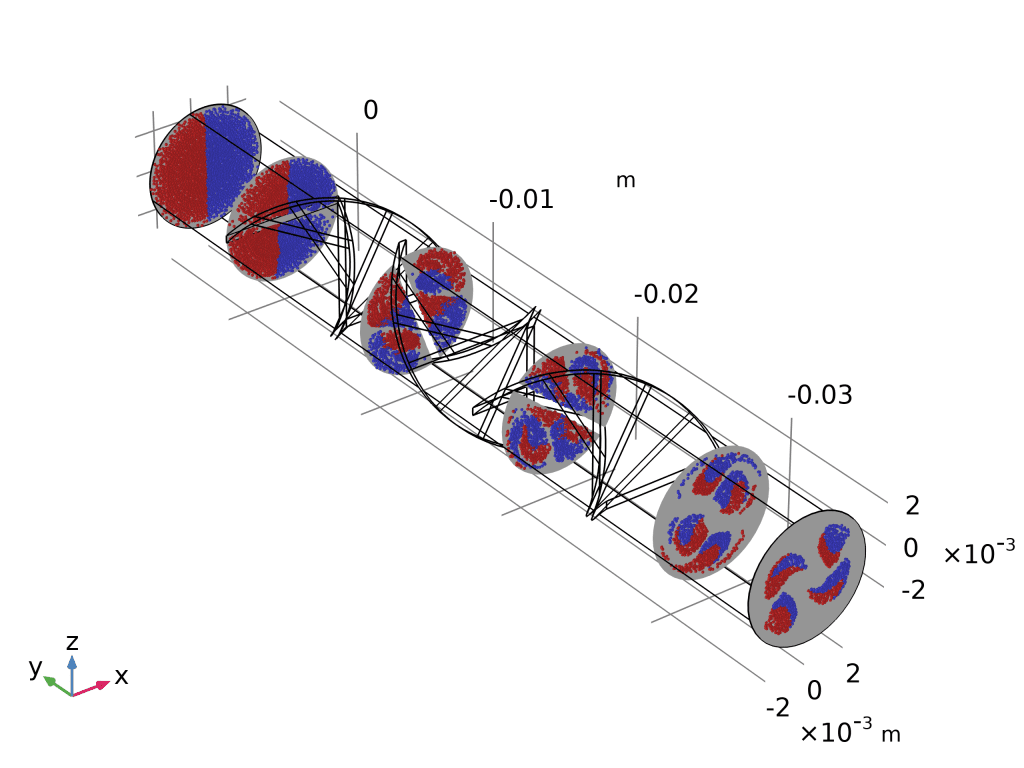
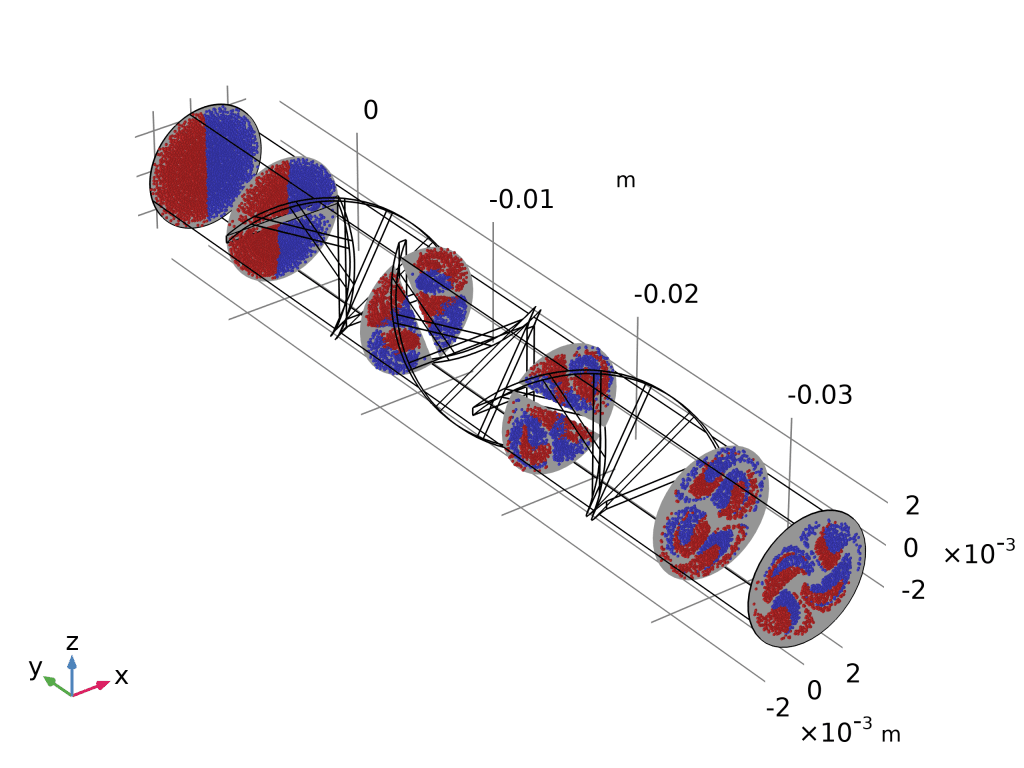
庞加莱图（Poincaré Map）：
- 先建“截面”数据集：yz-平面，沿程 5 个等距平面。
- 三维绘图组 → 庞加莱图 → 数据集选截面 → 粒子位置即与平面交点。
- 出口截面仍呈“红蓝分离”，量化证明还需增加扭曲叶片或延长流道。

3. 声学远场：把‘声压球’搬进报告

痛点：扬声器、声呐、超声换能器需要展示“声辐射指向性”，却苦于没有‘声音’云图。
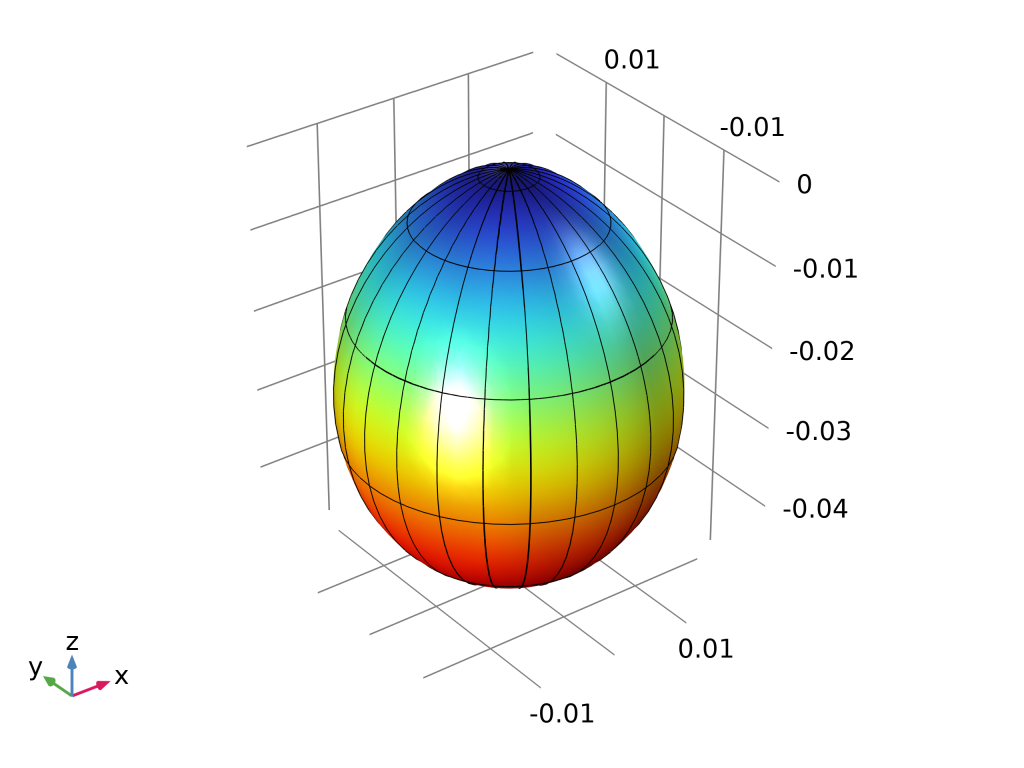
解决方案：同 RF 远场完全一致，只需把表达式换成声压 acpr.p_t 或声压级 acpr.Lp。
快速复刻：
1. 打开 “蘑菇头压电换能器”（声学模块 > Piezoelectric Devices）。
2. 远场图 → 表达式 acpr.Lp，频率 2 kHz。
3. 180 分辨率 → 得到一张“声压球”，高亮区域即主声束。
4. 论文 trick：把球面透明度调到 0.3，再叠一张切面云图， simultaneously show 3D directivity & 2D cross-section。

4. 极坐标 & 史密斯图：天线/微波人的“日常”

痛点：笛卡尔坐标看不出驻波、阻抗、反射系数真面目。
解决方案：
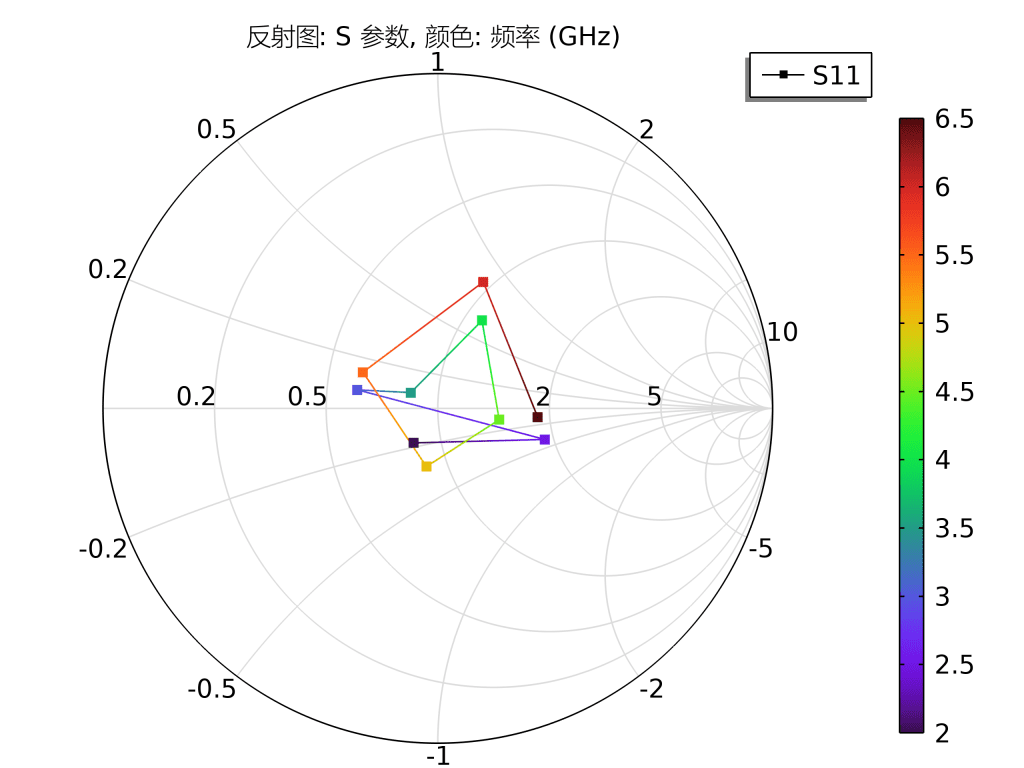
- 极坐标远场：结果 → 一维绘图组 → 极坐标图 → 选“Far-Field，2D”数据集 → 表达式 emw.normEfar，θ 扫描 0–360°——一张经典“花瓣”方向图立现。
- 史密斯图：同一维绘图组 → 史密斯图 → 端口阻抗 Z11 或 S 参数 S11——匹配点是否落在圆心一眼便知。

5. 动画 & 交互：把粒子‘演’给评委看

痛点：静态图无法展示瞬态混合、波束扫描、粒子漂移过程。
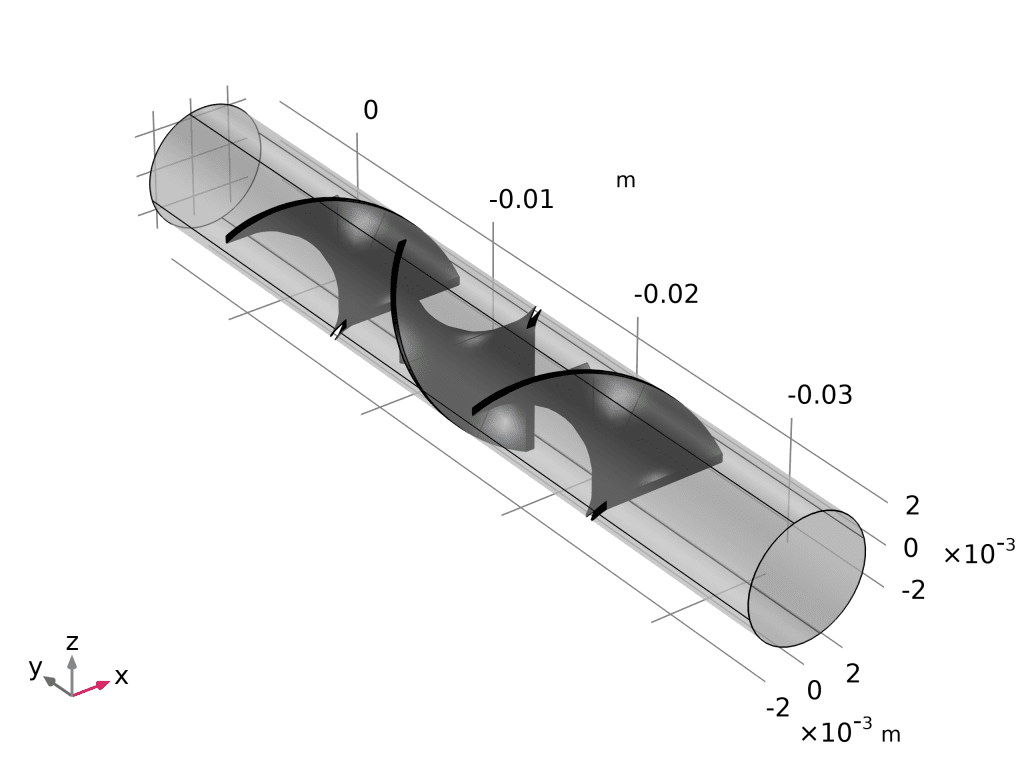
解决方案：用“播放器”或“导出动画”一键生成 .gif / .mp4。
实操：
1. 结果 → 导出 → 动画 → 播放器。
2. 主题选“Particle Trajectories”，帧数 100，速度 0.5×。
3. 点击播放，粒子像“彩色流星”沿混合器螺旋前进；暂停任意帧即可截取插图。
4. 会议 trick：导出 gif 循环播放，嵌入 PPT，无需切换软件即可现场演示。

结尾总结：

“到这里，你已解锁‘远场球’‘粒子雨’‘相图云’‘史密斯圆’——这些专用图表不再是论文里的‘别人家的孩子’。下一篇，我们将迎接最棘手的‘薄层结构’后处理：温度/应力/速度在边界上突然跳变？up、down、side 算子如何帮你拆穿‘假不连续’？终极篇，不见不散！”

发表回复取消回复