在有限元分析(FEA)或更广泛地,在偏微分方程(PDE)的数值模拟中,“源”(source)和“汇”(sink)是两个非常重要的概念,它们描述了系统内部或边界上物质的产生或消耗、能量的输入或输出、或更一般地,某种物理量的增加或减少机制。
✅ 一句话理解:
- 源(Source):使系统内某物理量增加的因素(正贡献)。
- 汇(Sink):使系统内某物理量减少的因素(负贡献)。
📌 数学上的体现
在控制方程中,源和汇通常出现在方程的右端项或边界条件中。
1. 在控制方程中
以热传导方程为例:
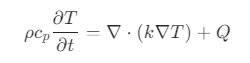
- Q 就是源项(source term):
- 如果 $ Q > 0 $:表示有热量产生(如电加热、化学反应放热)→ 源
- 如果 $ Q < 0 $:表示有热量被吸收(如冷却、相变吸热)→ 汇
2. 在边界条件中
例如,在对流边界条件中:
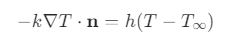
- 如果外界温度 T_∞ > T ,热量流入系统 → 源
- 如果 T_∞< T ,热量流出系统 → 汇
📌 有限元中的实现
在有限元离散中,源/汇项会被积分到单元右端向量(载荷向量)中。
示例:1D 热传导单元
假设单元长度为 L ,线性形函数为 N_1, N_2 ,源项为常数 Q :
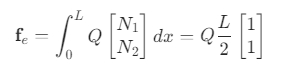
- 如果 Q > 0 :节点载荷为正 → 源
- 如果 Q < 0 :节点载荷为负 → 汇
📌 常见物理场景中的源/汇
| 物理场 | 源(Source)示例 | 汇(Sink)示例 |
|---|---|---|
| 热传导 | 电加热、化学反应放热 | 冷却、相变吸热 |
| 质量扩散 | 化学反应生成物质、注入 | 化学反应消耗物质、泄漏 |
| 流体流动 | 泵注入、质量源 | 泄漏、质量汇 |
| 电磁场 | 电流注入、电荷密度 | 电荷耗散、接地 |
| 结构力学 | 体积力(如重力、离心力) | 阻尼力(如粘滞阻尼) |
✅ 小结一句话:
在有限元中,源和汇是方程右端项或边界条件中,表示物理量增加或减少的机制,它们通过积分进入载荷向量,最终影响系统的响应。
如果你有具体的物理场(比如传热、流体、电磁、结构)或方程形式,我可以给你更具体的例子。

