在有限元仿真的教学体系中，教材习惯于把复杂物理 reality 拆解为几何形状规则、材料参数单一的“示范模型”，随后为它们逐一贴上“固定端”“对称面”“压力口”“绝热线”等多重边界条件，如同给每件家具贴上用途标签。学生若严格按图索骥，求解器便能顺利走完迭代；可一旦擅自删减、移位或合并某条边界，数值方程便立刻失衡——残差曲线飙升、矩阵奇异、甚至直接抛出“约束不足”或“过约束”的猩红提示。然而教材对这一幕几乎保持沉默：它只给出“应当如此”，却鲜少揭示“为何如此”——譬如哪条边界在扮演阻止刚体漂移的隐性锚点，哪对面在暗中平衡通量，哪条边又在为矩阵提供刚好足够的秩。于是，报错信息像一封没有译文的密信，令人困惑却无从拆解。

在学习了解这些问题之前，我们先要学习几个前提概念：

• 标量和矢量
• 场和势
• 有限元的迭代求解思路
• 第一类边界条件、第二类边界条件、第三类边界条件

标量、矢量

矢量是具有大小和方向的量，它可以用箭头表示。矢量的大小由其长度决定，而方向则由箭头的指向表示。例如，速度、力和位移都是矢量量。相反，标量是只具有大小而没有方向的量，它只用一个数值表示。例如，时间、温度和质量都是标量量。

矢量通常用粗体字母或带箭头的小写字母表示，如v、F和d。而标量则用普通的小写字母表示，如t、T和m。在数学运算中，矢量和标量之间的运算规则也不同。矢量之间可以进行加法、减法和乘法运算，而标量之间只能进行加法和乘法运算。

在某些情况下，矢量和标量可以组合在一起形成一个更复杂的量。例如，矢量的大小乘以标量可以得到一个新的矢量量。这在物理学中常用于描述力和位移之间的关系。另外，矢量的点乘和标量的乘法可以得到一个标量量，这在向量积分和能量计算中非常有用。

场和势

在有限元分析中，理解和区分“场”和“势”是非常重要的。以下是对这两个概念的解释：

场（Field）：在有限元分析中，“场”是指一个区域内物理量的分布，这些物理量可以是温度、位移、速度、压力等。场是空间和时间的函数，描述了在连续区域内这些物理量如何随位置和时间变化。例如，在热分析中，温度场描述了物体内部各点的温度分布；在结构分析中，位移场描述了结构在受力后各点的位移情况。

势（Potential）：“势”通常是指在某些物理问题中，场的产生原因或驱动力。在数学上，势可以被看作是一个标量函数，其梯度（或其他导数）给出了场。例如，在电静学中，电势是一个标量场，其负梯度给出了电场；在重力场中，重力势也是一个标量场，其梯度给出了重力场的方向和大小。

场与势的关系：场和势之间存在密切的关系。在某些情况下，场可以通过势的梯度来计算，这意味着场是势的空间变化率。例如，在静电学中，电场是电势的负梯度；在流体力学中，流速场是流函数的梯度。这种关系在有限元分析中非常重要，因为它允许我们通过求解势的方程来间接求解场的分布。

有限元的迭代求解思路

有限元法（FEM）是一种数值方法，它通过将连续的场离散化为一组在离散点上的值来近似求解偏微分方程。在有限元分析中，场和势的概念被用来构建近似方程，并通过数值方法求解这些方程。例如，有限元法可以用来计算电势分布，进而得到电场分布；或者计算温度势（温度场），进而分析热流。

总结来说，场描述了物理量在空间和时间上的分布，而势则是产生这些场的潜在原因。在有限元分析中，通过求解势的方程，我们可以间接求解场的分布，这对于理解和预测物理现象至关重要。

三类边界条件

在有限元分析中，理解边界条件是非常关键的，因为它们直接影响到求解偏微分方程的准确性和可靠性。通常，边界条件可以分为三类：狄利克雷（Dirichlet）边界条件、诺伊曼（Neumann）边界条件和罗宾（Robin）边界条件：

1. 狄利克雷边界条件

狄利克雷边界条件，也称为本质边界条件，用于指定求解区域边界上的因变量值。这种边界条件直接规定了物理量（如温度、位移等）在边界上的具体数值。例如温度。在热仿真中，这意味着在模型的某个边界上，温度是已知且固定的。例如，如果一个物体的表面与环境接触，并且我们知道这个表面的环境温度，就可以使用狄利克雷条件来指定这个温度值。在COMSOL Multiphysics中，狄利克雷条件会改变刚度矩阵的结构，因为它们指定了因变量，所以无须求解因变量。

2. 诺伊曼边界条件

诺伊曼边界条件，也称为自然边界条件，用于指定边界上的通量，即因变量的法向导数。这种边界条件涉及物理量的空间变化率，在热仿真中，这通常指的是热通量，也就是热量通过边界的速率。例如，如果一个物体的表面正在以已知的速率散热，就可以使用诺伊曼条件来指定这个热通量。在COMSOL Multiphysics的方程视图中，诺伊曼条件显示为弱贡献，纯粹是方程组右侧附加的贡献

3. 罗宾边界条件

罗宾条件结合了狄利克雷和诺伊曼条件的特点，用于指定变量及其梯度之间的关系。在热仿真中，罗宾条件通常用于模拟对流，其中边界上的温度和热通量通过一个系数（如对流换热系数）联系起来。例如，如果一个物体的表面与流体接触，并且对流传热是主要的热交换机制，就可以使用罗宾条件来描述这种关系

总结来说，狄利克雷边界条件指定了边界上的因变量值，诺伊曼边界条件指定了边界上的通量，而罗宾边界条件则结合了前两者，指定了变量和通量之间的关系。在实际应用中，根据具体问题的物理背景和边界特性，选择合适的边界条件类型是非常重要的。

三类边界条件用数学角度总结是：

• 第一类边界条件：给出求解变量在边界上的数值；
• 第二类边界条件：给出求解变量在边界外法线的方向导数；
• 第三类边界条件：给出求解变量在边界上的参考值和外法向导数的线性组合。

在有限元仿真中，我们大多数场景下，都是通过对仿真模型施加以上三种类型的边界条件来进行有限元仿真求解的，但是怎样的组合才是一个有效的组合？让我们在一个简单的热学仿真场景中对以上问题进行理解。

现在假设有一根1 m长的铝材质的金属棒，在棒子的圆柱表面都为绝热边界（没有热交换的边界），仅靠棒两头的热边界情况控制整体的温度条件，将这个模型转化有限元仿真中，我们可以将其简化为一个一维的热传导仿真。

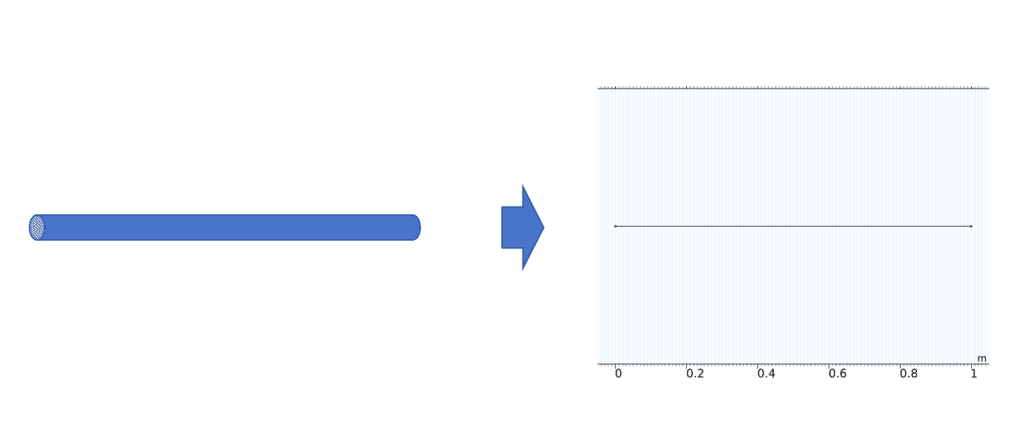
接下来将棒两端的热边界条件，分别考虑成三种边界条件下的实际类型：

• 第一类边界条件：对边界给定温度，对应实际物理场景下端口被控制成恒定温度（100℃或者25℃）
• 第二类边界条件：对边界给定给定通量情况下，指定了（Q=10 [W/m2]）
• 第三类边界条件：对边界给给定了一个参考温度和一个参考通量，比如对流换热类型下，末端边界处于一个外部环境温度为25℃，换热系数为 5 W/m2/K的对流传热边界条件。

以下表格列出了两端边界条件为不同边界条件类型下的边界条件实例条件。

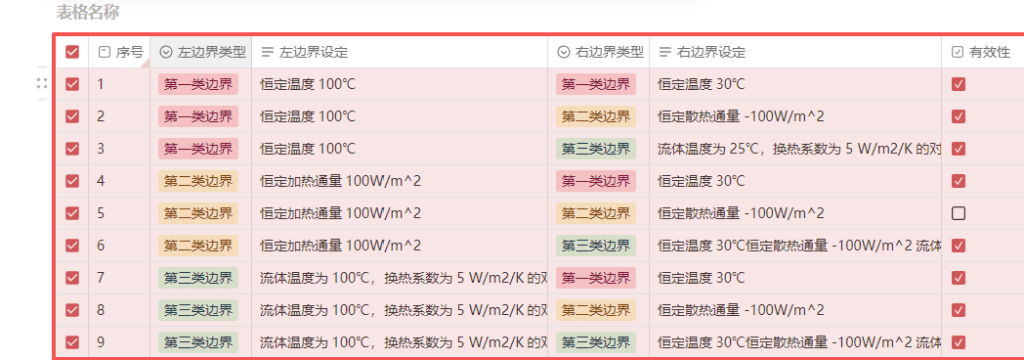
请分别思考以上不同条件下的可行性，以下初始温度为25℃情况下的稳态仿真结果：

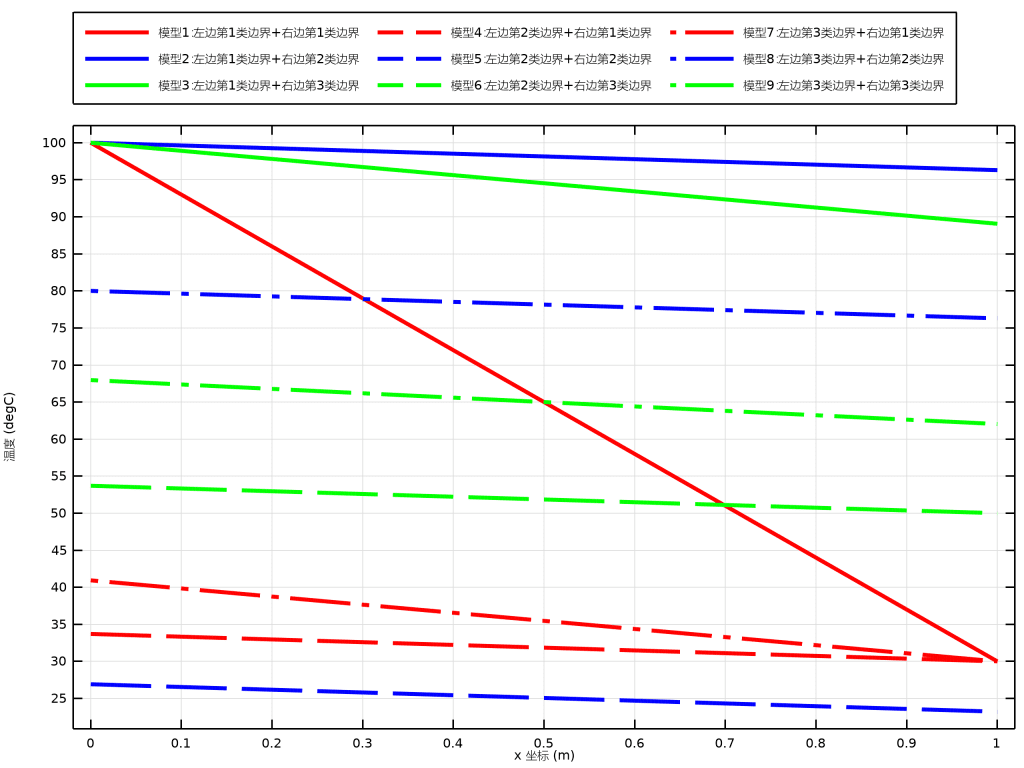
其中模型5的结果，是一个非收敛解，在这个模型的求解过程中，软件提示：

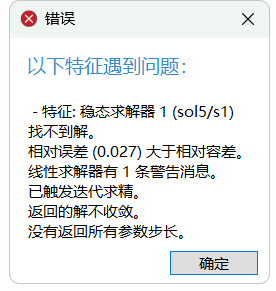
但是我们在模型5的结果中却得到一个有温度梯度，两端温度不平衡的数值分布结果，这是为什么呢？

为什么其他条件都可以求解，而两端都是第二类边界条件就不能求解呢？因为在这样的设定条件下，整个求解区域没有一个可以参考的温度势，因为在两端给定的这个热通量情况下，只能求解得到两端的温度差是指定的，而没法确定这个温度差是基于什么实际的温度分布，目前的解是仅基于初始温度25℃下获得的无数个满足边界条件的解中的一个，而实际上，而其实当中间的平均温度为100℃ 时候，也可以满足当前的边界条件设定。

源

上面的案例假设条件中：“在铝棒的圆周表面是没有换热计算的”

https://cn.comsol.com/blogs/how-to-make-boundary-conditions-conditional-in-your-simulation

COMSOL Multiphysics 的“后处理”往往被当成锦上添花的一步，实则却是决定仿真价值能否真正落地的“最后一公里”。初学COMSOL的用户往往在“后处理”环节陷入“数据堆砌”的困境：颜色泛滥、图窗杂乱、关键物理量彼此掩盖，最终难以用一张图讲清故事。针对这一痛点，为了让“数据”顺利升格为“信息”，再沉淀为“洞察”，这篇博文将给出一条可复制的“零代码”后处理流水线，详尽地介绍 COMSOL 中的各种后处理形式，包括：

• 基本绘图与表达式: 涵盖创建自定义表达式、使用派生值（如全局计算、平均值）验证模型、绘制网格图来评估网格质量等。
• 高级可视化技巧: 包括使用变形、高度表达式和缩放来增强可视化效果，以及利用截面、截线、合并数据集和过滤器来聚焦和分析特定区域的结果。
• 专用绘图类型: 介绍了针对特定物理场的绘图，如射频（RF）分析的远场图和粒子追踪图。
• 降维后处理: 针对薄层结构，详细讲解了如何处理和解释在边界（二维）上绘制体（三维）结果时可能出现的“不连续性”，并介绍了up、down和side 算子的使用。
• 视图、相机与灯光控制: 说明了如何通过调整视角、相机位置和多种光源（定向光、点光源、聚光灯）来创建更具表现力和清晰度的图像。
• 动画与结果导出: 简要提及了如何创建动画并导出结果。

分步规划：

• 第一篇：基础篇——《数据“体检”与表达：如何确保你的仿真结果值得信赖？》
  • 核心内容：聚焦仿真结果的基础验证与核心绘图表达。
  • 关键技巧：自定义表达式、派生值（全局计算）、网格质量评估。
• 第二篇：技巧篇——《让图像“说话”：提升仿真图表现力的核心技巧》
  • 核心内容：介绍增强可视化效果的通用技巧。
  • 关键技巧：变形、高度表达式、缩放、视图与相机控制、灯光与场景设置。
• 第三篇：高级篇——《洞察与聚焦：如何深度剖析你的仿真数据？》
  • 核心内容：讲解如何对数据进行降维、切片和聚焦分析。
  • 关键技巧：截面与截线、合并数据集、过滤器。
• 第四篇：专业篇——《专业图表与特殊应用：满足你的“小众”需求》
  • 核心内容：介绍针对特定物理场的专用绘图类型。
  • 关键技巧：远场图（RF/声学）、粒子追踪图（庞加莱图、相图）。
• 第五篇：挑战篇——《破解“不连续”之谜：薄层结构后处理的终极指南》
  • 核心内容：深度解析薄层结构中的降维后处理问题。
  • 关键技巧：理解边界与域图差异、掌握up、down和side 算子。

第一篇：数据“体检”与表达

标题：

吃透 COMSOL 后处理（一）：数据“体检”与表达——如何确保你的仿真结果值得信赖？

开篇引言：

“当你的仿真结果新鲜出炉，你是否也曾感到无从下手？面对五彩斑斓的云图，除了‘看起来不错’，我们如何确信它真的反映了物理世界的真相？今天，我们将从最基础也是最核心的步骤开始，学习如何像医生一样，为你的仿真数据做一次全面的‘体检’，并掌握表达核心信息的语言。”

正文核心：

1. 自定义表达式：让软件绘制你真正关心的物理量

• 痛点：默认的物理量列表（如温度、应力）有时无法满足我们的分析需求。例如，在电磁-热耦合分析中，你可能想直接观察“焦耳热功率密度”的分布，以确定电路板上的热点。
• 解决方案：COMSOL 允许你像写数学公式一样，手动输入任意表达式。
• 实操案例：

1. 打开 COMSOL 案例库中的“母线板（Busbar）”模型。
2. 添加一个“三维绘图组”，在“表面”图中，将表达式从默认的ec.normJ（电流密度模）改为自定义表达式ec.Jx*ec.Ex + ec.Jy*ec.Ey + ec.Jz*ec.Ez。

3.对比：你会发现，这个手动输入的表达式与软件预定义的ec.Qrh（电阻损耗）结果完全一致。这验证了我们表达式的正确性。

• 进阶技巧：
  • 解构分析：我们可以进一步将焦耳热公式拆解，分别绘制ec.Jx*ec.Ex和ec.Jy*ec.Ey。通过对比，你会发现热量主要集中在 X 方向的电流路径上，而 Y 和 Z 方向的贡献微乎其微。这种“解构”能力是自定义表达式最强大的地方，它能帮你洞察现象背后的主导因素。

ec.Jx*ec.Ex

ec.Jy*ec.Ey

2. 派生值：用几个关键数字，为模型做一次“体检”

• 痛点：云图只能提供定性的视觉感受。如何快速、定量地验证模型的正确性？答案是通过计算一些关键的“派生值”。
• 核心思想：利用全局计算（Global Evaluation）来检查最基本的物理守恒定律是否满足。
• 实操案例：
  1. 打开“散热器（Heat Sink）”模型。能量守恒检查：在“结果”下的“派生值”中，添加一个“全局计算”。在表达式中输入ht.ntefluxInt（总净能量速率）。计算结果应非常接近于你施加在模型上的总热功率（例如1W）。如果计算结果是0.99996 W，那就证明能量在系统内是守恒的，你的模型在能量层面是可信的。
  操作路径：模拟开发器窗口下—结果节点下—右击“派生值”选择并单击“全局计算”—在设置窗口找到“表达式”栏在输入框里输入ht.ntefluxInt
• 质量守恒检查：再添加一个“全局计算”，输入表达式spf.out1.Mflow（质量流）。将这个值与入口速度、流体密度和入口面积手动计算出的理论质量流量进行对比。如果两者非常接近，则证明质量也是守恒的。操作路径：模拟开发器窗口下—结果节点下—右击“派生值”选择并单击“全局计算”—在设置窗口找到“表达式”栏在输入框里输入spf.out1.Mflow
• 价值：派生值是验证模型正确性的“试金石”。只有当这些基本物理量都守恒时，我们才能对后续的复杂分析有信心。

3. 网格图：为你的“画布”做一次质量评估

• 痛点：再漂亮的云图，如果建立在一张粗糙、扭曲的“画布”（网格）上，其结论也是不可靠的。因此，后处理的第一步，往往是从检查网格本身开始。
• 解决方案：创建一个“网格图”，无需任何求解结果，即可直观地查看网格单元的质量和尺寸分布。
• 实操案例：
  1. 在“散热器”模型的“网格”节点上，直接点击“绘制”。解读：在生成的网格图中，颜色通常代表单元质量（Quality），范围为0到1。红色区域表示质量差（细长、扭曲）的单元。如果高应力、高梯度区域恰好位于这些红色单元上，那么你需要重新细化网格，否则结果可能失真。

价值：网格图是“事前诸葛”，它能帮助你在进行复杂分析之前，就发现并修正潜在的数值误差源头，避免“垃圾进，垃圾出”的悲剧。

结尾总结：

“至此，我们已经完成了对仿真数据的基础‘体检’。我们学会了如何‘说’出自己关心的物理量，用几个关键数字验证了模型的基本功，并检查了我们所依赖的‘画布’——网格——的质量。这是所有后续高级分析的地基。下一篇，我们将进入‘美工’阶段，学习如何让这些可信的数据，变成一张震撼、清晰、能打动人心的图像。敬请期待！”